センター試験数学IA 2007年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 方程式
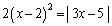 ・・・①
・・・①
を考える。
(1) 方程式①の解のうち、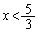 を満たす解は
を満たす解は 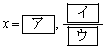
である。 (2) 方程式①の解は全部で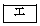 個ある。その解のうちで最大のものをαとすると、
個ある。その解のうちで最大のものをαとすると、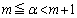 を満たす整数mは
を満たす整数mは である。
である。
[2] 集合A,Bを


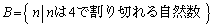
とする。
(1) 次の と
と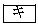 に当てはまるものを、下の
に当てはまるものを、下の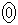 ~
~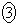 のうちから一つずつ選べ。
のうちから一つずつ選べ。 自然数がnがAに属することは、nが2で割り切れるための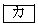 。
。
自然数がnがBに属することは、nが20で割り切れるための 。
。  必要十分条件である
必要十分条件である
 必要条件であるが、十分条件でない
必要条件であるが、十分条件でない
 十分条件であるが、必要条件でない
十分条件であるが、必要条件でない
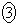 必要条件でも十分条件でもない
必要条件でも十分条件でもない(2) 次の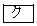 ~
~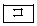 に当てはまるものを、下の
に当てはまるものを、下の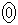 ~
~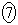 のうちから一つずつ選べ。
のうちから一つずつ選べ。 とする。自然数全体の集合を全体集合とし、その部分集合Gの補集合を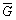 で表すとき
で表すとき である。
[解答へ]
[2] aを定数とし、xの2次関数
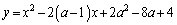 ・・・①
・・・①
のグラフをGとする。
(1) グラフGが表す放物線の頂点の座標は
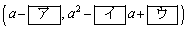
である。グラフGがx軸と異なる2点で交わるのは
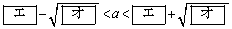
のときである。さらに、この二つの交点がともにx軸の負の部分にあるのは
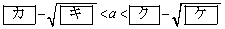
のときである。
(2) グラフGが表す放物線の頂点のx座標が3以上7以下の範囲にあるとする。
このとき、aの値の範囲は
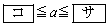
であり、2次関数①の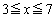 における最大値Mは
における最大値Mは
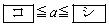 のとき
のとき
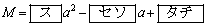
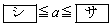 のとき
のとき

である。
したがって、2次関数①の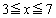 における最小値が6であるならば
における最小値が6であるならば

であり、最大値Mは

である。 [解答へ]
[3] 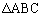 において、
において、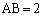 ,
,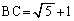 ,
,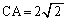 とする。また、
とする。また、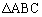 の外接円の中心をOとする。
の外接円の中心をOとする。
(1) このとき、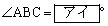 であり、外接円Oの半径は
であり、外接円Oの半径は 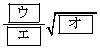
である。 (2) 円Oの円周上に点Dを、直線ACに関して点Bと反対側の弧の上にとる。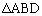 の面積を
の面積を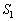 ,
,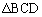 の面積を
の面積を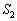 とするとき
とするとき 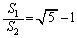 ・・・①
・・・①
であるとする。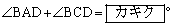 であるから
であるから
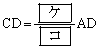
となる。このとき
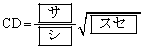
である。
さらに、2辺AD,BCの延長の交点をEとし、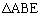 の面積を
の面積を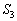 ,
,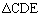 の面積を
の面積を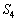 とする。このとき
とする。このとき
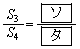 ・・・②
・・・②
である。①と②より
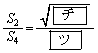
となる。 [解答へ]
[4] 1辺の長さ1の正六角形があり、その頂点の一つをAとする。一つのさいころを3回投げ、点Pを次の(a),(b),(c)にしたがって、この正六角形の辺上を反時計回りに進める。
(a) 頂点Aから出発して、1回目に出た目の数の長さだけ点Pを進める。
(b) 1回目で点Pがとまった位置から出発して、2回目に出た目の数の長さだけ点Pを進める。
(c) 2回目で点Pがとまった位置から出発して、3回目に出た目の数の長さだけ点Pを進める。
(1) 3回進めたとき、点Pは正六角形の辺上を1周して、ちょうど頂点Aに到達する目の出方は 通りである。
通りである。 3回進める間に、点Pが1回も頂点Aにとまらない目の出方は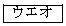 通りである。
通りである。
(2) 3回進める間に、点Pが3回とも頂点Aにとまる確率は であり、ちょうど2回だけ頂点Aにとまる確率は
であり、ちょうど2回だけ頂点Aにとまる確率は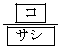 である。
である。 3回進める間に、点Pがちょうど1回だけ頂点Aにとまる確率は である。
である。
(3) 3回進める間に、点Pが頂点Aにとまる回数の期待値は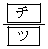 回である。
回である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 