�@���ʃe�X�g���w IA '26 �N�� 1 ��@ [1] �@�S�̏W�� U �� 2 �ȏ� 20 �ȉ��̎��R���S�̂̏W���Ƃ���B���Ȃ킿
�ł���B 2 �ȏ� 9 �ȉ��̎��R�� a �C b �ɑ��āA U �̕����W�� A �C B ��
�Ƃ���B
�ł���B
(1) �̂Ƃ��A �C �ł���B ( �������̂��J��Ԃ��I��ł��悢�B ) �@
(2) a �C b �� 2 �ȏ� 9 �ȉ��̎��R���ł��邱�Ƃɒ��ӂ��āA a �C b �ɂ��čl���悤�B
(i) �̗v�f�ɁA 2 �̔{���� 3 �̔{�����Ȃ��Ƃ� �ł���B
(ii) �ł���Ƃ� �C �ł���B
[2] �@�ȉ��̖��ɂ����Ĕ������ꍇ�́A�ł��ȒP�Ȑ����̔�œ�����B
(1) �l�p�` ABCD �̖ʐ� S �ɂ��čl���悤�B�ȉ��ł́A�l�p�` ABCD �̓��p A �C B �C C �C D �ŕ\���B�������A�l�̓��p�͂������ �Ίp�� BD �����ʂ� 1 �ӂƂ��遢 ABD �Ɓ� BCD �̖ʐς��A���ꂼ�� �C �ƂȂ�B ABCD �̎l�̓��p�� �@����@ �ƂȂ�B ( �������̂��J��Ԃ��I��ł��悢�B ) �@ �̉Q �@ �̉Q �@
(2) �_ O �𒆐S�Ƃ��锼�a 6 �̉~ O ���A���� PQ ��� P �C Q �ƈقȂ�_ M �ɂ����Đ��� PQ �ɐڂ��Ă���B P �C Q ���ꂼ���ʂ�~ O �̐ڐ��ŁA���� PQ �ƈقȂ���̂������A���̉~�Ƃ̐ړ_�����ꂼ�� K �C L �Ƃ���B�ȉ��ł͒��� PK �C QL �������ꍇ���l���A���̌�_�� R �Ƃ���B���̂Ƃ��A�� PQR �̕ӂ̒����ɂ��čl���悤�B
(i) �C 2 ���� PK �C QL �̌�_ R �͒��� PQ �Ɋւ��ē_ O �Ɠ������ɂ���B �l�p�` PMOK ���� PMO �Ɓ� PKO �ɕ������邱�Ƃɒ��ӂ���ƁA�l�p�` PMOK �̖ʐς� QLOM �ɂ��Ă����l�ɍl����ƁA PR �F QR �� �F PQR �̕ӂ̒��������߂邱�Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@ [2] �͏��X�Y�ނ����m��܂���B���ɍŌ�̃q�t�w�́A�ǂ��� 4 �_�ŁA���Ԃ��l����ƁA�p�X���ăJ���Ń}�[�N������������ł��B�q�t�w���l�m�n�Ɠ����}�[�N�ɂ����l�͖{���Ƀ��b�L�[�ł����A�o��ɕs���N�Ȃ��̂���������܂���B [1] �@ A �́A �W�� U �̗v�f�̂����ŁA a �̈��������̒��ɏo�Ă���f�� ( �������邱�Ƃ�����܂� ) �̔{���̏W���A B �́A�W�� U �̗v�f�̂����ŁA b �̈��������̒��ɏo�Ă���f���̔{���̏W���ł� ( ���� ���Q�� ) �B (1) �̂Ƃ��A A �́A U �̂����� 3 �̔{���A�܂�A B �́A U �̂����� 2 �̔{���A�܂�A 6 �@�C 8 ......[ �� ] �́A 3 �� 2 �̌��{���ŁA 3 �̔{���ł����ċ����łȂ� ( �܂� ) ���̂ŁA 3 �@�G 2 ......[ �� ]
(2)(i) �� 2 �̔{���ł� 3 �̔{���ł��Ȃ��A�Ƃ����̂́A A �� 2 �̔{���� 3 �̔{�������킹���W�����Ƃ������Ƃł��B�܂�A A �́A 1 �ȊO�̐��̌��������̏W�����Ƃ������Ƃł��B�@�I 6 ......[ �� ] (ii) �Ƃ������Ƃ́A A �̗v�f�ɂ� 5 ���܂܂��Ƃ������ƂŁA B �� 5 ���܂݂܂���B A �� 5 �̔{���̏W�����Ƃ��āA 5 ���܂ނ��A 10 �C 15 �C 20 ���܂݂܂���B�Ƃ������Ƃ́A B �� 5 ���܂܂��A 10 �C 15 �C 20 ���܂݂܂��B�����Ȃ�̂� (i) ��� 5 �@�L 6 ......[ �� ]
[2](1) �E�}��� ( �O�p�`�̖ʐ� ���Q�� ) �A 1 �@�P 4 ......[ �� ] ���A 4 ......[ �� ] ���A �T 2 ......[ �� ]
�� PKO = �� PMO �� PMOK �̖ʐς́A 7 �@�X 2 ......[ �� ] �l�p�` PMOK �́A ( �~�Ɛ}�` ���Q�� ) �̂ŁA PMOK �̖ʐρ� PKM �{�� OKM �� 72 �ł��邱�Ƃ���A �� �@�Z 4 �@�\ 5 ......[ �� ] �l�p�` QLOM �̖ʐρ� QLO �{�� QMO �� �� �@�^�` 12 �@�c�e 13 ......[ �� ] �� PQR �̖ʐςɂ��āA �g�i 15 �@�j�k 13 ......[ �� ] �Ƃ��āA �� �@�l�m 21 �@�n 2 ......[ �� ] (ii) (i) �Ɠ��l�ɂ��āA�l�p�` PMOK �͉~�ɓ��ڂ��A �l�p�` PMOK �̖ʐρ� PKO �{�� PMO �́A PMOK �̖ʐς��� PKM �{�� OKM �ƌ��āA �� �l�p�` QMOL �̖ʐρ� QLO �{�� QMO �́A QMOL �̖ʐς��� QLM �{�� OLM �ƌ��āA �� ���A�� PQR �̖ʐςɂ��āA �@�q�t 21 �@�w 2 ......[ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� �Ȃ��A�́A © 2005-2026 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 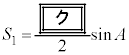 �C
�C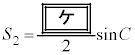
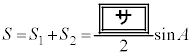 �@����@
�@����@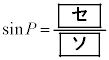 �ƂȂ邱�Ƃ��킩��B
�ƂȂ邱�Ƃ��킩��B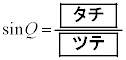 �ƂȂ邱�Ƃ��킩��B����āAPR�FQR ��
�ƂȂ邱�Ƃ��킩��B����āAPR�FQR �� 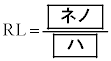 �Ƌ��߂���̂ŁA��PQR�̕ӂ̒��������߂邱�Ƃ��ł���B
�Ƌ��߂���̂ŁA��PQR�̕ӂ̒��������߂邱�Ƃ��ł���B