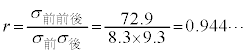�@���ʃe�X�g���w IA '26 �N�� 2 ��@ [1] �@ 2 �����̍ő�l�A�ŏ��l�ɂ��čl���悤�B
(1) 2 ����
(2) ���Y����ƉԎq����́A (1) ��U��Ԃ��� 2 �����̍ő�l�A�ŏ��l�ɂ��Ęb���Ă���B
���Y�F (1) �ł́A 2 ������ x �̎�蓾��l�͈̔͂��^�����āA�ő�l�ƍŏ��l�����߂邱�Ƃ��ł����ˁB
�Ԏq�F���Ⴀ�A x �̒l�͈̔͂Ƃ��̂Ƃ��̍ő�l�ƍŏ��l�Ɋ��������^�����Ă���ꍇ�ɁA�������� 2 ���������߂邱�Ƃ͂ł���̂��ȁB��̓I�ȗ�ōl���Ă݂悤�B
(i) 2 ���� ���� 1 �����Ƃ���B �| ���� 1 �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�� �E 3 ���Ƃ�B �E �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| �ł���B �@ �@ �@ �@
(ii) 2 ���� ���� 2 �����Ƃ���B �| ���� 2 �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
a �𐳂̒萔�Ƃ��A M �C�ŏ��l�� m �Ƃ���� �E �E �E �E �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| 2 ���� �ł���B �@���ɓʁ@�@ �̉Q �@
(3) 2 ���� ���� 3 �����Ƃ���B �| ���� 3 �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
b ��萔�Ƃ��A M �Ƃ���� �E �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| ���Y�F (2) �� ���� 1 �� ���� 2 ����͊�����Ɍ��܂������ǁA ���� 3 �����ł́A �Ԏq�F�ł��A x ���̋��L�_�̍��W�͂킩�肻�����ˁB
2 ���� x ���̋��L�_�� x ���W�� [2] �@�ȉ��̖�������ɂ������ẮA�^����ꂽ�f�[�^�ɑ��āA���̒l���O��l�Ƃ���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�u ( �� 1 �l���ʐ� ) �| 1.5 �~ ( �l���ʔ͈� ) �v�ȉ��̒l ( �� 3 �l���ʐ� ) �{ 1.5 �~ ( �l���ʔ͈� ) �v�ȏ�̒l
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| 1500m ���R�`�ɂ�����y�[�X�z�����l���邽�߂ɁA 2021 �N�ɊJ�Â��ꂽ�����I�����s�b�N�̒j�q 1500m ���R�`�Ɋւ���f�[�^�͂��邱�Ƃɂ����B�Ȃ��A���R�`�Ƃ́A�ǂ̂悤�ȉj�����ʼnj���ł��悢���Z�̂��Ƃł���B 28 �l�̑I��ɂ�����A�\�I�Ōv�����ꂽ�L�^ ( �ȉ��A�^�C�� ) �Ƃ���B�����ł́A�^�C���͕b�P�ʂŕ\�����̂Ƃ���B�Ⴆ�A 15 �� 23 �b 46 �ł���A ( �b ) �ł���B�����āA�������� ( �ȉ��A���� ) �́A�^�C���̒l��������������ʂƂȂ�B�܂��A 28 �l�̑I�肻�ꂼ��̃^�C���ɂ��āA�X�^�[�g���� 750m �܂ł̃^�C���� 750m ����S�[���܂ł̃^�C���� (1) ���Y����́A 1 �� 2 �́A 1 �Ɛ} 2 �ɂ����āA A ��t���Ă���_�́A�����I��ł��邱�Ƃ�\���Ă���B ���� (a) �C (b) �́A�} 1 �Ɛ} 2 �Ɋւ���L�q�ł���B
(a) �� 470 �b�����ł���I��ɂ��āA 460 �b�ȏ�ł���I��̐l���ƁA 460 �b�ȏ�ł���I��̐l���͓������B (b) A ��t���Ă���_���\���I��ɂ��āA
(2) ���Y����́A 1 �̂悤�ɁA���ϒl�A�W��������ы����U�����߂��B �@�\ 1 �@ �@ ���ϒl�@ �W�����@ �����U�@ 450 8.3 72.9 453 9.3
�\ 1 ��p����ƁA �@ 0.01 �@�@ 0.24 �@�@ 0.47 �@�@ 0.59 �@�@ 0.72 �@ 0.83 �@�@ 0.94 �@�@ 1.06 �@�@ 1.38 �@�@ 4.14
(3) ���Y����́A���ʂƃy�[�X�z���̊W�ׂ邽�߂ɁA�O���ƌ㔼�Ƃ����������ł͂Ȃ��A���ׂ����������ꂽ�^�C����p���ĕ��͂��邱�Ƃɂ����B 1500m ���R�`�̃^�C���́A�X�^�[�g���� 50m �܂ł̃^�C���A 50m ���� 100m �܂ł̃^�C���̂悤�ɁA�S�[���܂� 50m ���Ƃ� 30 �ɕ����Čv������Ă���B�����ŁA����� 30 �̃^�C����p���ĕ��͂���B
(i) 1 �ʂ̑I��� 30 �̃^�C���ɂ��čl����ƁA�O��l���ǂ����f�����̒l�ł��� 29.315 �� 29.835 ���Z�o����A 29.315 �ȉ��� 2 �̃^�C���� 29.835 �ȏ�� 1 �̃^�C�����O��l�Ɣ��f���ꂽ�B���̂Ƃ��A 1 �ʂ̑I��� 30 �̃^�C���̎l���ʔ͈͂� 0. �b�ł���B (ii) ���Y����� 28 �l�̑I�肻�ꂼ��ɂ��āA 30 �̃^�C����p���āA�I�育�Ƃ̔��Ђ��}���쐬���A���U���v�Z�����B�} 3 �͏ォ�番�U���������Ȃ�悤�ɁA 28 �l�̑I�肻�ꂼ��̔��Ђ��}����ׂ����̂ł���A 30 �̃^�C���ɂ�����O��l�́A���ۂŎ�����Ă���B�Ȃ��A���U���������I��͂��Ȃ������B ���� (a) �C (b) �́A�} 3 �Ɋւ���L�q�ł���B
(a) 28 �l�̑I��ɂ��āA 29 �b��葬���^�C���͂��ׂĊO��l�ł���B
(b) 28 �l�̑I�肩�� 2 �l��I�Ƃ��A���U�̑傫���I��̎l���ʔ͈͂́A���U�̏������I��̎l���ʔ͈͂�菬�������Ƃ�����B
(iii) ���ʂ� 1 �ʂ��� 8 �ʂ܂ł̑I��̃O���[�v�������i�o�O���[�v�A 9 �ʂ��� 28 �ʂ܂ł̑I��̃O���[�v��\�I�s�ރO���[�v�ƌĂԂ��Ƃɂ���B�����i�o�O���[�v�ł���A���� 30 �̃^�C���̕��U�������������� 14 �Ԗڂ܂ł̑I��̐l���� n (�l ) �Ƃ���ƁA�\ 2 �̂悤�ɂȂ�B
�@�\ 2 �@���ʂƕ��U�̕\ �@ �@���U ( �������� ) �@ �v 1 �ԁ` 14 �� 15 �ԁ` 28 �� ���� �����i�o�O���[�v �@ n 8 �\�I�s�ރO���[�v 20 �v �@ 14 �@ �@ 14 �@ 28
���̂Ƃ��A�} 3 ���� 14 �Ԗڂ̑I�肪��߂銄���� P �C�\�I�s�ރO���[�v�ɂ����ĕ��U�������������� 14 �Ԗڂ܂ł̑I�肪��߂銄���� Q �Ƃ���ƁA ���@�@ �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@ [1] �� 2 ���� �́A���������p�o���ƈႤ�p�x����Ȃ̂ł��˘f�������m��܂���B [2] �͊�{�I�ŕ��ՁA���w���ł�������ꂻ���ł��B [1](1) �̃O���t�́A ( 2 �����̍ő�ŏ� ���Q�� ) �B�@�A 0 �@�C 5 �@�E 2 �@�G�I �| 3 ......[ �� ]
(2)(i) �ő�l�����ʒu���͈� 2 �����̎��ʒu�� 3 �Ȃ̂ŁA���_�̍��W�� 3 ......[ �� ] �@�� �@�L�N �| 2 �@�P 4 �@�R 1 ......[ �� ]
(ii) �Ȃ�� 2 �����ł��̃O���t�͉��ɓʂł��B�@�T 0 ......[ �� ] �O���t�� �@�V 6 ......[ �� ]
(3) �̂Ƃ��A�Ⴆ�A M �� M �� M �� �̂Ƃ��A M �� b �� 1 ��菭���ł��������Ȃ�ƁA M �� x �� 2 ��菭���傫���� ( 2 ���������̉��̔z�u ���Q�� ) �B M �� b �� 7 ��菭���ł��傫���Ȃ�ƁA M �� x �� 6 ��菭���傫���� x ���̋��L�_�� x ���W�́A 2 �� 6 �ł��B�@�X 2 �@�Z 6 ......[ �� ] [2] �@�O��l�́A�� 1 �l���ʐ� �� 3 �l���ʐ��� ( �� 1 �l���ʐ� ) �| 1.5 �~ ( �l���ʔ͈� ) �v�ȉ��̒l �@����@ �u ( �� 3 �l���ʐ� ) �{ 1.5 �~ ( �l���ʔ͈� ) �v�ȏ�̒l �@����A �����܂��B
(1)(a) �} 1 ������ƁA 7 �l�ł��B�} 2 ������ƁA 3 �l�ł��B���҂͓���������܂���B���ł��B (b) �} 1 �C�} 2 ������ƁA�I�� A �� �\ 2 ......[ �� ]
(2) �� r �́A �^ 6 ......[ �� ]
(3)(i) �l���ʔ͈͂� x �Ƃ���ƁA��L�� �@���A �@�`�c 13 ......[ �� ]
(ii)(a) �} 3 ������ƁA�ォ�� 26 �Ԗڂ� 17 �ʂ̑I��܂ł́A 29 �b��葬���^�C���͂��ׂĊO��l�ł����A�ォ�� 27 �Ԗڂ� 26 �ʂ̑I��Əォ�� 28 �Ԗڂ� 21 �ʂ̑I��ɂ��ẮA�ŏ��l�� 28 �b�����������̂ɔ��ۂ����Ă��炸�A�O��l�ɂȂ��Ă��܂���B�Ƃ������Ƃ́A 29 �b���������^�C�������ׂĊO��l�Ƃ͌����܂���B���ł��B
(b) 4 �ʂ̑I��� 12 �ʂ̑I��A 9 �ʂ̑I��� 20 �ʂ̑I��A 7 �ʂ̑I��� 5 �ʂ̑I��A 11 �ʂ̑I��� 22 �ʂ̑I�������ƁA���U�̑傫���I��̎l���ʔ͈͂��A���U�̏������I��̎l���ʔ͈͂����������Ȃ��Ă��܂��B�������B
�e 2 ......[ �� ]
(iii) �����i�o�O���[�v (1 �ʁ` 8 �� ) �̂��� 14 �Ԗڂ܂ł� 7 �I�肪����A 15 �ԁ` 28 �Ԃ� 7 �ʂ̑I�� 1 �l������܂��B����āA�\ 2 ���A 7 ......[ �� ] �����i�o�O���[�v�ł́A 8 �l���A 7 �ʂ̑I������� 7 �l�����U�̏����������� 14 �Ԗڂ܂łɓ����Ă��܂��B 20 �l���A 14 �ʁA 12 �ʁA 20 �ʁA 9 �ʁA 19 �ʁA 15 �ʁA 24 �ʂ� 7 �I�肪 14 �Ԗڂ܂łɓ����Ă��܂��B 2 ......[ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� �Ȃ��A�́A © 2005-2026 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� ��