�@���ʃe�X�g���wIA '26�N��3��@
 ��ԓ��ɁA
��ԓ��ɁA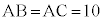 �C
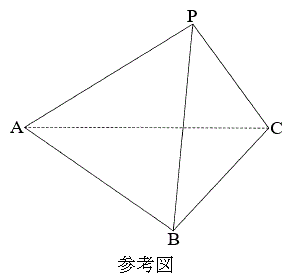
�C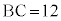 �ł���ӎO�p�`ABC������B��ABC�̓��S��I�Ƃ��A��IBC�̏d�S��G�Ƃ���BG��ʂ�A��ABC���܂ޕ��ʂƐ����Ȓ�����ɁAG�ƈقȂ�_P������B���̂Ƃ��A��ABC���ʂƂ���O�p��PABC�ɂ��čl���悤�B
�ł���ӎO�p�`ABC������B��ABC�̓��S��I�Ƃ��A��IBC�̏d�S��G�Ƃ���BG��ʂ�A��ABC���܂ޕ��ʂƐ����Ȓ�����ɁAG�ƈقȂ�_P������B���̂Ƃ��A��ABC���ʂƂ���O�p��PABC�ɂ��čl���悤�B
����AI�ƕ�BC�̌�_��D�Ƃ��A�܂��A��PA��̓_E�́A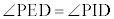 �����Ă���Ƃ���B�Ȃ��A�ȉ��̖��ɂ����Ĕ������ꍇ�́A�ł��ȒP�Ȑ����̔�œ�����B
�����Ă���Ƃ���B�Ȃ��A�ȉ��̖��ɂ����Ĕ������ꍇ�́A�ł��ȒP�Ȑ����̔�œ�����B
(1) ����BI�� ���Ƃɒ��ӂ���ƁA��ABD�ɂ����Đ���AI��ID�̒����̔�����߂邱�Ƃ��ł���B����āA����AD�̒����ɒ��ڂ����
���Ƃɒ��ӂ���ƁA��ABD�ɂ����Đ���AI��ID�̒����̔�����߂邱�Ƃ��ł���B����āA����AD�̒����ɒ��ڂ���� 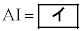 �C
�C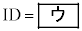
�ł��邱�Ƃ��킩��B�܂��A4�_E�CI�CD�C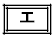 �͓���~����ɂ���B�����
�͓���~����ɂ���B����� �ł��邱�Ƃ��킩��B
 �̉Q
�̉Q 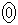 �@����AC�Ɛ����Ɍ����
�@����AC�Ɛ����Ɍ����
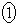 �@����AC�Ƃ˂���̈ʒu�ɂ���
�@����AC�Ƃ˂���̈ʒu�ɂ���
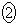 �@
�@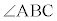 ��2��������
��2��������
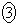 �@��AC�̒��_��ʂ�
�@��AC�̒��_��ʂ� �̉Q
�̉Q �@A�@�@
�@A�@�@ �@B�@�@
�@B�@�@ �@C�@�@
�@C�@�@ �@G�@�@
�@G�@�@ �@P
�@P
(2) ����PI��DE�̌�_��F�Ƃ���B���̂Ƃ��A����IF��FP�̒����̔�ƁA�O�p��PABC�ё̐ςƂ̊W�ɂ��čl���悤�B
(i) ��������1�̂��ƂŎO�p��PABC�̑̐�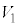 �ɂ��čl����B
�ɂ��čl����B
�|����1�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
����IF��FP�̒����̔䂪IF�FFP �� 3�F2�ł���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���̂Ƃ�
PE�FEA ��  �F
�F
�ł��邩��A(1)�ł̍l�@�ɒ��ӂ���ƁA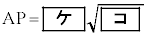 �ƂȂ�B
�ƂȂ�B
���������āA����PG����ABC���܂ޕ��ʂɐ����ł��邱�Ƃɒ��ӂ���ƁA �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B
(ii) (i)������1�̑���Ɏ�������2�������A�O�p��PABC�̑̐ς̕ω��ɂ��čl����B
�|����2�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
����IF��FP�̒����̔䂪IF�FFP �� 1�F3�ł���B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
����2�̂��Ƃł̎O�p��PABC�̑̐�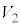 ���A(i)�ŋ��߂�
���A(i)�ŋ��߂�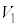 �Ɣ�r����ƁA
�Ɣ�r����ƁA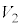 ��
��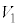 �̔��
�̔�� �ł��邩��A �B
�B
 �̉Q
�̉Q 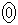 �@
�@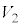 ��
��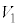 ��菬����
��菬����
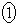 �@
�@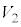 ��
��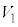 �͓�����
�͓�����
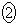 �@
�@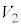 ��
��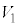 ���傫��
���傫��
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̐}�`�ƕ��ʐ}�`������݂����Ă��āA�C�Â��ɂ�������������܂��B������ŗ��������āA������Ƃ����}��`�����Ƃ���ł��B
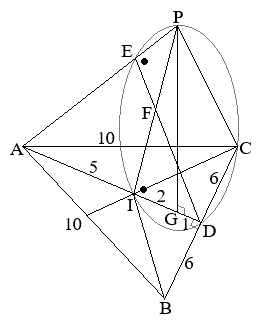 ��ABC�͓ӎO�p�`�Ȃ̂ŁAAD�́A
��ABC�͓ӎO�p�`�Ȃ̂ŁAAD�́A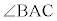 �̓����ł���Ɠ����ɁAD��BC�̒��_�ŁA
�̓����ł���Ɠ����ɁAD��BC�̒��_�ŁA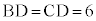 �ł��B�܂��A
�ł��B�܂��A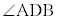 �͒��p�ŁA�O�����̒藝���A
�͒��p�ŁA�O�����̒藝���A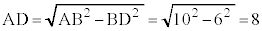 �ł��B
�ł��B
(1) ����BI��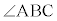 �̓����ł�(�O�p�`�̌ܐS���Q��)�B�@�A 2 ......[��]
�̓����ł�(�O�p�`�̌ܐS���Q��)�B�@�A 2 ......[��] ������ABA�FBD �� AI�FID = 10�F6�C����āA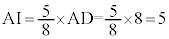 �C
�C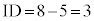 �ł��B�@�C 5�@�E 3 ......[��]
�ł��B�@�C 5�@�E 3 ......[��]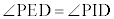 �Ȃ̂ŁA�~���p�̒藝�̋t���A�l�p�`EIDP�͉~�ɓ��ڂ���l�p�`�ł��B�@�G 4 ......[��]���ׂ��̒藝���A
�Ȃ̂ŁA�~���p�̒藝�̋t���A�l�p�`EIDP�͉~�ɓ��ڂ���l�p�`�ł��B�@�G 4 ......[��]���ׂ��̒藝���A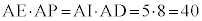 �@����@
�@����@
�I�J 40 ......[��]
����āA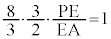 �@��
�@�� 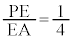 �@�L 1�@�N 4 ......[��]
�@�L 1�@�N 4 ......[��]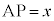 �Ƃ����
�Ƃ����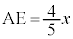 �C�@���A
�C�@���A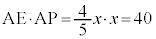 �@��
�@�� 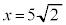 �@�P 5�@�R 2 ......[��]
�@�P 5�@�R 2 ......[��]
G�́�IBC�̏d�S�Ȃ̂ŁAIG�FGD �� 2�F1�ł��B �Ȃ̂ŁA
�Ȃ̂ŁA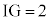 �ł���A
�ł���A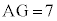 �ł��B�O�����̒藝���A
�ł��B�O�����̒藝���A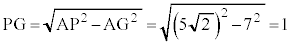
��ABC�̖ʐς́A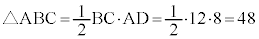
�O�p��PABC�̑̐�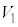 �́A
�́A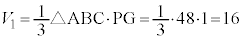 �@�T�V 16 ......[��]
�@�T�V 16 ......[��]
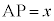 �Ƃ����
�Ƃ����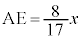 �C�@���A
�C�@���A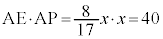 �@��
�@�� 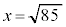 �O�����̒藝���A
�O�����̒藝���A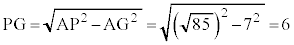
��ABC�̖ʐς�48��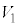 �ƕς�炸�A
�ƕς�炸�A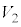 �F
�F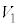 �� 6�F1�@�X 6�@�Z 1 ......[��]
�� 6�F1�@�X 6�@�Z 1 ......[��]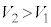 �ł��B�@�\ 2 ......[��]
�ł��B�@�\ 2 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B