�@���ʃe�X�g���w IA '26 �N�� 4 ��@ 1 �l�� 1 �l�őΐ킷�鋣�Z�̑�����A A �C B �C C �� 3 �l�A�܂��� A �C B �C C �C D �� 4 �l�ŊJ�Â����B���̓��[�O��`���ōs����B���Ȃ킿�A���ꂼ��̐l�����̑S�Ă̐l�� 1 �ΐ킷��B���������͂Ȃ����̂Ƃ��A A ���ΐ푊��ɏ��m���� A �ȊO�� 2 �l���ΐ킷��Ƃ����m���͂ǂ���� �D���҂̌��ߕ� �ɂ��D���҂� 1 �l���߂�B �D���҂̌��ߕ� �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| ����������ԑ����l�� 1 �l�ł���A���̐l��D���҂Ƃ���B�����łȂ���A���I�ɂ��A����������ԑ����l�̒����� 1 �l��I�сA���̐l��D���҂Ƃ���B�������A����������ԑ����l�̐l���� n �l�ł���Ƃ��A���ꂼ��̐l���I���m���� �|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�| A ���D������m�����A A �C B �C C �� 3 �l�Ń��[�O����s���Ƃ��ƁA A �C B �C C �C D �� 4 �l�Ń��[�O����s���Ƃ��ƂŔ�r���悤�B �ΐ팋�� �ƌĂԁB�Ȃ��A �ΐ팋�� �͒��I�̌��ʂ��܂܂Ȃ��B �ΐ팋�� ���������߂ɕ\��p����B�Ⴆ�A�\ 1 �� 4 �l�Ń��[�O����s�����Ƃ��� �ΐ팋�� �̈�������B A ����n�܂�s�́~�Z�Z�́A A �� B �ɕ��� C �� D �ɏ����A 2 �� 1 �s�ƂȂ������Ƃ������B�܂��A����������ԑ��� A �� B �� 2 �l�����I�̑Ώۂł���A���̂��Ƃ� ✓ �Ŏ����B 1 �_ A B C D ������ ������ ���I A �_ �~ �Z �Z 2 1 ✓ B �Z �_ �Z �~ 2 1 ✓ C �~ �~ �_ �Z 1 2 �| D �~ �Z �~ �_ 1 2 �|
(1) A �C B �C C �� 3 �l�Ń��[�O����s���Ƃ��� A ���D������m�����l����B
(i) A �� 2 �� 0 �s�Ȃ�A A ���D������B A �� 2 �� 0 �s�ŗD������m����
(ii) A �� 1 �� 1 �s�ŗD�����邽�߂ɂ́A B �� C �� 1 �� 1 �s�ł��邱�Ƃ��K�v�ł���B�Ⴆ�A A �������肪 B �ł���Ƃ��A A �� C �ɕ��� B �� C �ɏ����Ƃ��K�v�ł���B�\ 2 �́A���� �ΐ팋�� �������A���� �ΐ팋�� �ɂȂ�m���� A �����I�ɂ��D���҂ɑI���m����
�@�@�@�@�\�@ 2 �_ A B C ������ ������ ���I A �_ �Z �~ 1 1 ✓ B �~ �_ �Z 1 1 ✓ C �Z �~ �_ 1 1 ✓
�@ A ��������� B �C C �� 2 �ʂ肠�邱�Ƃɒ��ӂ���ƁA A �� 1 �� 1 �s�ŗD������m���� (i) �� (ii) ����A A ���D������m���� (2) A �C B �C C �C D �� 4 �l�Ń��[�O����s���Ƃ��� A ���D������m�����l����B
A �� 3 �� 0 �s�Ȃ�A A ���D������B�܂��A A �� 1 �� 2 �s�Ȃ�A 2 ���ȏシ��l�����邽�� A �͗D�����Ȃ��B A �� 2 �� 1 �s�ŗD������m�����A�S�s����l������ꍇ�̊m���ƑS�s����l�����Ȃ��ꍇ�̊m���̘a�Ƃ��ċ��߂�B
(i) �S�s����l������ꍇ�ŁA���� A �� 2 �� 1 �s�ŗD������m�������߂�B
�S�s����l�� B �C C �C D �� 3 �ʂ肠��B�Ⴆ�A D ���S�s����Ƃ��A �ΐ팋�� �̈ꕔ�������ƕ\ 3 �̂悤�ɂȂ�B 3 �_ A B C D ������ ������ ���I A �_ �@ �@ �Z �@ �@ �@ B �@ �_ �@ �Z �@ �@ �@ C �@ �@ �_ �Z �@ �@ �@ D �~ �~ �~ �_ 0 3 �|
�@ D ���S�s����m���� D ���S�s����ꍇ�A A �� 2 �� 1 �s�ŗD�����邽�߂ɂ́A A �� D �ȊO�� 2 �l�Ƃ̑ΐ�� 1 �� 1 �s�ƂȂ邱�Ƃ��K�v�ł���B (1) �� (ii) �̌��ʂ�p���A�S�s����l�� B �C C �C D �� 3 �ʂ肠�邱�Ƃɒ��ӂ���ƁA�S�s����l������ꍇ�ŁA���� A �� 2 �� 1 �s�ŗD������m����
(ii) �S�s����l�����Ȃ��ꍇ�ŁA���� A �� 2 �� 1 �s�ŗD������m�������߂�B
A �� 2 �� 1 �s�̂Ƃ��A A �������鑊��� B �C C �C D �� 3 �ʂ肠��B�Ⴆ�A A �������鑊�肪 B �ł���Ƃ��A �ΐ팋�� �̈ꕔ�������ƕ\ 4 �̂悤�ɂȂ�B 4 �_ A B C D ������ ������ ���I A �_ �~ �Z �Z 2 1 �@ B �Z �_ �@ �@ �@ �@ �@ C �~ �@ �_ �@ �@ �@ �@ D �~ �@ �@ �_ �@ �@ �@
���̂Ƃ��A
A ���D�����邽�߂ɂ́A B �� 2 �� 1 �s�� 1 �� 2 �s�ł��邱�Ƃ��K�v�ł���B�Ⴆ�A�\ 1 �́A A �� B �� 2 �� 1 �s�ł��� �ΐ팋�� �̈�������A A �� B �� 2 �l�����I�̑ΏۂƂȂ������Ƃ������B 1 �@ ( �Čf ) �_ A B C D ������ ������ ���I A �_ �~ �Z �Z 2 1 ✓ B �Z �_ �Z �~ 2 1 ✓ C �~ �~ �_ �Z 1 2 �| D �~ �Z �~ �_ 1 2 �|
�S�s����l�����Ȃ��ꍇ�ŁA���� A �� B �ɕ��� C �� D �ɏ����D������Ƃ��� �ΐ팋�� �� A �������鑊�肪 B �C C �C D �� 3 �ʂ肠�邱�Ƃɒ��ӂ���ƁA�S�s����l�����Ȃ��ꍇ�ŁA���� A �� 2 �� 1 �s�ŗD������m���� (i) �� (ii) ����A A �� 2 �� 1 �s�ŗD������m���� A �� 3 �� 0 �s�ŗD������m�����l������ƁA A ���D������m���� (1) �ŋ��߂� 3 �l�Ń��[�O����s���Ƃ��� A ���D������m����� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@���ł͂���܂��A��₱������ɉr���o�߂̊m�F������ŁA�g�ɂ��܂��͂܂�Ȃ��Ƃ��ȂǁA������ł͌����Ƃ����Ȃ����[���ɒ��ӂ��Ȃ������K�v������܂��B (1)(i) A �� 2 ������ �m�� �́A 4 �@�C 9 ......[ �� ]
(ii) A �� 1 �� 1 �s�ƂȂ�m���́A B �� C �ɏ��m���� 2 �̑ΐ팋�ʂƂȂ�m���́A 1 �@�G 9 ......[ �� ] �\ 2 �̑ΐ팋�ʂƂȂ�A���� A �� 3 �l�̒��I�ɂ��D���҂ƂȂ�m���́A ( �@�I 1 �@�J 3 ......[ �� ] A �������肪 B �C C �� 2 �ʂ肠��̂ŁA A �� 1 �� 1 �s�ŗD������m���́A 2 �@�N�P 27 ......[ �� ] �� (ii) ����A A ���D������m���́A (2) A �� 3 �� 0 �s�ŗD������m���́A
(i) D ���S�s����m���� D �� A �ɕ�����m���� 1 �@�T 6 ......[ �� ] D ���S�s�����Ƃ��A A �� 2 �� 1 �s�ɂȂ�m���́A A �� B �ɕ����� (B �� C �ɕ����� ) �� C �ɕ����� (C �� B �ɕ����� ) ���� 2 �ʂ肠��A 3 �ʂ肠��A�S�s����l������ꍇ�A 2 �� 1 �s�̐l�� 3 �l����̂ŁA 3 �l�̒��I�ɏ����� A �� 2 �� 1 �s�ŗD������m���́A 1 �@�X�Z 27 ......[ �� ]
(ii) �S�s����l�����Ȃ��ꍇ�ŁA���� A �� B �ɕ��� C �� D �ɏ��ΐ팋�ʂ́A
B �Z - �~ C �C B �~ - �Z D �C C �Z - �~ D(B �F 2 �� 1 �s�A C �F 1 �� 2 �s�A D �F 1 �� 2 �s ) �~ - �Z C �C B �Z - �~ D �C C �~ - �Z D(B �F 2 �� 1 �s�A C �F 1 �� 2 �s�A D �F 1 �� 2 �s ) �~ - �Z C �C B �~ - �Z D �C C �Z - �~ D(B �F 1 �� 2 �s�A C �F 2 �� 1 �s�A D �F 1 �� 2 �s ) �~ - �Z C �C B �~ - �Z D �C C �~ - �Z D(B �F 1 �� 2 �s�A C �F 1 �� 2 �s�A D �F 2 �� 1 �s ) �� 4 �ʂ�B�@�\ 4 ......[ �� ] �C C �C D �ɂ��đΐ팋�ʂ������Ȃ�m���́A A �� B �ɕ��� C �� D �ɏ��m���́A A �������鑊��́A B �C C �C D �� 3 �ʂ肠��A 2 �� 1 �s�̐l�� 2 �l����̂ŁA 2 �l�̒��I�ɏ����� A �� 2 �� 1 �s�ŗD������m���́A 1 �@�` 9 ......[ �� ] �� (ii) ����A A �� 2 �� 1 �s�ŗD������m���́A A ���D������m���́A 4 �@�e 9 ......[ �� ] ���̊m���� (1) �ŋ��߂� 3 �l�Ń��[�O����s���Ƃ��� A ���D������m���@���A 2 �@�i�j 27 �@�k 0 ......[ �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� �Ȃ��A�́A © 2005-2026 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� ��  �ł���B
�ł���B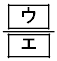 �ł���B���̑ΐ팋�ʂɂȂ�A����A�����I�ɂ��D���҂ɑI���m����
�ł���B���̑ΐ팋�ʂɂȂ�A����A�����I�ɂ��D���҂ɑI���m����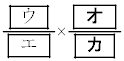 �ł���B
�ł���B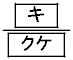 �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B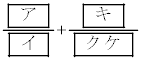 �ł���B
�ł���B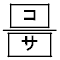 �ł���BD���S�s����ꍇ�AA��2��1�s�ŗD�����邽�߂ɂ́AA��D�ȊO��2�l�Ƃ̑ΐ��1��1�s�ƂȂ邱�Ƃ��K�v�ł���B
�ł���BD���S�s����ꍇ�AA��2��1�s�ŗD�����邽�߂ɂ́AA��D�ȊO��2�l�Ƃ̑ΐ��1��1�s�ƂȂ邱�Ƃ��K�v�ł���B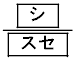 �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B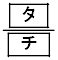 �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B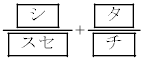 �ł���B
�ł���B �ł��邱�Ƃ��킩��B���̊m����(1)�ŋ��߂�3�l�Ń��[�O����s���Ƃ���A���D������m�����
�ł��邱�Ƃ��킩��B���̊m����(1)�ŋ��߂�3�l�Ń��[�O����s���Ƃ���A���D������m�����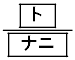 ����
����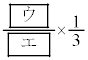 (
(