共通テスト数学IIBC '26年第1問
Oを原点とする座標平面において、方程式
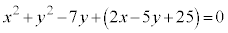 ・・・①
・・・①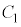 とする。また、方程式
とする。また、方程式
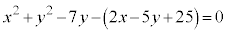 ・・・②
・・・②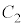 とする。
とする。
(1) 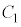 の中心の座標は
の中心の座標は である。
である。 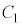 の半径を
の半径を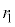 ,
,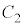 の半径を
の半径を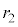 ,
,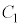 の中心と
の中心と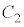 の中心の間の距離をdとすると、
の中心の間の距離をdとすると、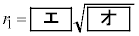 ,
,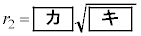 ,
, である。
である。
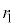 ,
,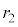 ,dの関係から、
,dの関係から、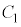 と
と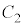 は2点で交わることがわかる。
は2点で交わることがわかる。
(2) 不等式
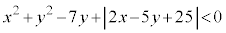 ・・・③
・・・③の表す領域について考える。
③の左辺は、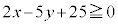 のときは①の左辺と一致し、
のときは①の左辺と一致し、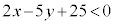 のときは②の左辺と一致する。
のときは②の左辺と一致する。
(i) 不等式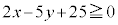 の表す領域をD,不等式
の表す領域をD,不等式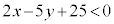 の表す領域をEとする。
の表す領域をEとする。 ・原点Oは に含まれる。
に含まれる。 ・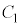 の中心は
の中心は に含まれる。
に含まれる。 ・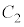 の中心は
の中心は に含まれる。
に含まれる。  ~
~ の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)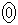 D
D 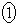 E
E
(ii) 方程式
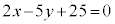 ・・・④
・・・④の表す直線を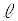 とする。
とする。
実数x,yが①と②の両方を満たすとする。①と②の左辺どうし、右辺どうしの差をとると となる。よって、実数x,yは④も満たす。
したって、 。このことから、
。このことから、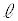 は
は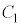 と
と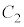 の二つの交点を通る直線であることがわかる。
の二つの交点を通る直線であることがわかる。
 については、最も適当なものを、次の
については、最も適当なものを、次の ~
~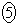 のうちから一つ選べ。
のうちから一つ選べ。 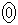 点Pを
点Pを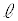 上の点とすると、Pは
上の点とすると、Pは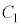 上にあり、かつ
上にあり、かつ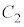 上にもある
上にもある 点Pを
点Pを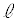 上の点とすると、Pは
上の点とすると、Pは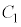 上にあるか、または
上にあるか、または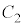 上にある
上にある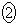 点Pを
点Pを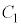 上にあり、かつ
上にあり、かつ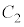 上にもある点とすると、Pは
上にもある点とすると、Pは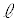 にある
にある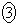 点Pを
点Pを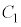 上にあるか、または
上にあるか、または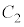 上にある点とすると、Pは
上にある点とすると、Pは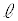 にある
にある 点Pを
点Pを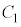 上の点、点Qを
上の点、点Qを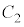 上の点とすると、直線PQは
上の点とすると、直線PQは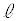 と一致する
と一致する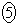 点Pを
点Pを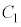 上の点、点Qを
上の点、点Qを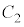 上の点とすると、直線PQは
上の点とすると、直線PQは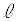 と交わる
と交わる
(iii) 不等式
の表す領域と(i)の領域Dの共通部分をFとする。
また、不等式
の表す領域と(i)の領域Eの共通部分をGとする。
不等式③の表す領域は、FとGの和集合である。これを図示すると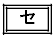 の灰色部分である。ただし、境界線を含まない。
の灰色部分である。ただし、境界線を含まない。
(iv) ③において、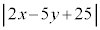 の前の符号を+から-に変えた不等式
の前の符号を+から-に変えた不等式 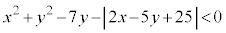 ・・・⑤
・・・⑤を考える。⑤の表す領域を図示すると の灰色部分である。ただし、境界線を含まない。
の灰色部分である。ただし、境界線を含まない。
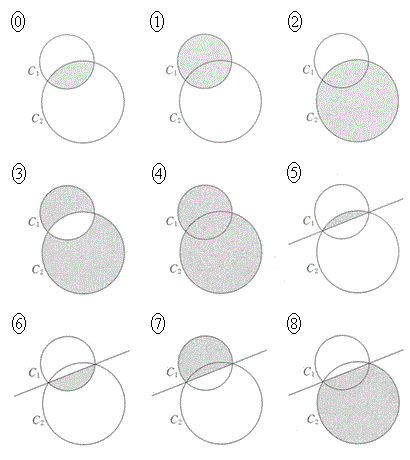
 ,
, については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、
のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよい。なお、 ~
~ では座標軸を省略している。
では座標軸を省略している。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円 と領域の基本問題で、この問題は落とせません。
(1) ①を変形すると、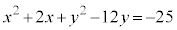
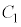 :
: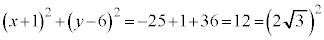
②を変形すると、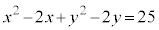
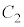 :
: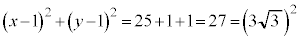
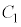 の中心の座標は
の中心の座標は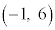 アイ -1 ウ 6 ......[答]
アイ -1 ウ 6 ......[答]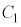 の半径
の半径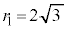 エ 2 オ 3 ......[答]
エ 2 オ 3 ......[答]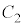 の半径
の半径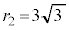 カ 3 キ 3 ......[答]
カ 3 キ 3 ......[答]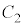 の中心は
の中心は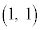 ,
,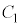 ,
,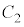 の中心間距離
の中心間距離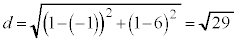 クケ 29 ......[答]
クケ 29 ......[答]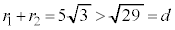 より、
より、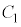 ,
,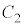 は2点で交わります(2円の位置関係を参照)。
は2点で交わります(2円の位置関係を参照)。
(2) 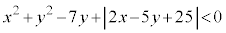 ・・・③
・・・③
(i) D: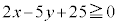
E: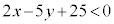 DとEには共通部分はありません。
DとEには共通部分はありません。 ・原点O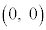 の座標は、
の座標は、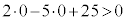 よりDを満たすので、原点OはDに含まれます。 コ 0 ......[答]
よりDを満たすので、原点OはDに含まれます。 コ 0 ......[答] ・ の中心
の中心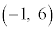 は、
は、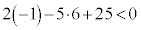 よりEを満たすので、
よりEを満たすので、 の中心
の中心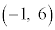 はEに含まれます。 サ 1 ......[答]
はEに含まれます。 サ 1 ......[答] ・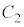 の中心
の中心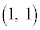 は、
は、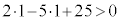 よりDを満たすので、
よりDを満たすので、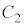 の中心
の中心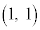 はDに含まれます。 シ 0 ......[答]
はDに含まれます。 シ 0 ......[答] (ii)  :
: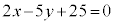 ・・・④
・・・④ 実数x,yが①,②の両方を満たすとき、①-②より、
より、実数x,yは④も満たし、 上にあり、かつ
上にあり、かつ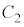 上にある点Pは
上にある点Pは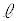 上にもあります。 ス 2 ......[答]領域Dは、直線
上にもあります。 ス 2 ......[答]領域Dは、直線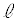 から下側の領域です。領域Eは、直線
から下側の領域です。領域Eは、直線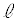 よりも上側の領域です。
よりも上側の領域です。
(iii) 不等式: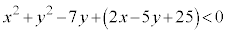 ,即ち、
,即ち、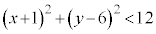 の表す領域は、円
の表す領域は、円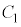 より内側です。これと領域Dとの共通部分Fは、円
より内側です。これと領域Dとの共通部分Fは、円 より内側であって直線
より内側であって直線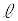 から下側の部分です。
から下側の部分です。 不等式: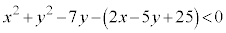 ,即ち、
,即ち、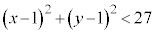 の表す領域は、円
の表す領域は、円 より内側です。これと領域Eとの共通部分Gは、円
より内側です。これと領域Eとの共通部分Gは、円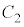 より内側であって直線
より内側であって直線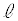 より上側です。
より上側です。
不等式③の表す領域、つまり、FとGの和集合は、円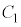 より内側と円
より内側と円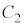 より内側の共通部分に一致します。 セ 0 ......[答]
より内側の共通部分に一致します。 セ 0 ......[答]
(iv) 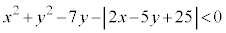 ・・・⑤
・・・⑤ D: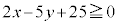 のとき、⑤は、
のとき、⑤は、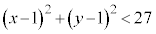 となり、円
となり、円 より内側の領域とDとの共通部分で、円
より内側の領域とDとの共通部分で、円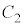 より内側であって直線
より内側であって直線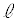 から下側です。E:
から下側です。E: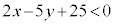 のとき、⑤は、
のとき、⑤は、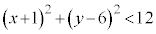 となり、円
となり、円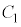 より内側の領域とEとの共通部分で、円
より内側の領域とEとの共通部分で、円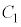 より内側であって直線
より内側であって直線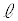 より上側です。
より上側です。
不等式⑤の表す領域を図示すると、両者の和集合であって、円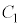 より内側と円
より内側と円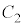 より内側を合わせた部分に一致します。 セ 4 ......[答]
より内側を合わせた部分に一致します。 セ 4 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2026(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。