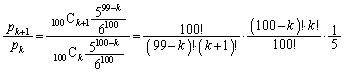�c�嗝�H���w'08�N[A2]
(1) ��������𑱂���n����Ƃ��A6�̖̖ڂ����o��m����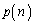 �Ƃ���B���Ƃ��A
�Ƃ���B���Ƃ��A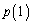 ��
��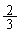 �C
�C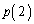 ���@�J�@�ł���B
���@�J�@�ł���B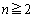 �̂Ƃ�
�̂Ƃ�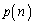 ��
��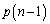 �̊Ԃɂ�
�̊Ԃɂ�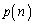 ���@�L�@�Ƃ����W�������藧�B������n��p����
���@�L�@�Ƃ����W�������藧�B������n��p����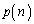 ������킷��
������킷��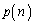 ��
��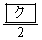 �ł���B
�ł���B (2) ��������𑱂���100����Ƃ��A1�̖ڂ����傤��k�� (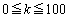 )�o��m����
)�o��m����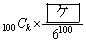 �ł���A���̊m�����ő�ɂȂ�̂�k���@�R�@�̂Ƃ��ł���B
�ł���A���̊m�����ő�ɂȂ�̂�k���@�R�@�̂Ƃ��ł���B ���ɁA��������𑱂���n����Ƃ��A1�̖ڂ����傤��k�� (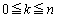 )�o��m�����l����Bn���Œ肵���Ƃ��A���̊m�����ő�ɂ���悤��k�̒l��2���݂��邽�߂̕K�v�\�������́An���@�T�@�Ŋ������Ƃ��̗]�肪�@�V�@�ƂȂ邱�Ƃł���B
)�o��m�����l����Bn���Œ肵���Ƃ��A���̊m�����ő�ɂ���悤��k�̒l��2���݂��邽�߂̕K�v�\�������́An���@�T�@�Ŋ������Ƃ��̗]�肪�@�V�@�ƂȂ邱�Ƃł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� ���̖���[A1]�Ɠ��l�A���}�ȕp�o�p�^�[���̖��ł��B(�R)��k��o��m����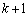 ��o��m���̔���l���܂��B
��o��m���̔���l���܂��B
(1)(�J) ���������2���āA6�̖̖ڂ����o��̂́A1��ڂ�1�C2�C3�C6���o�āA2��ڂ�4�C5���o�邩�A1��ڂ�4�C5���o�āA2��ڂ�1�C2�C3�C6���o��ꍇ�ŁA�����m���́A 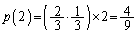 ......[��]
......[��]
(�L) n��ڂ܂łŁA6�̖̖ڂ����o��̂́A
(i) 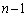 ��ڂ܂łŁA6�̖̖ڂ����o�āAn��ڂ�4�C5���o��A���A
��ڂ܂łŁA6�̖̖ڂ����o�āAn��ڂ�4�C5���o��A���A (ii) 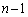 ��ڂ܂łŁA6�̖̖ڂ�������o�āAn��ڂ�1�C2�C3�C6���o��A
��ڂ܂łŁA6�̖̖ڂ�������o�āAn��ڂ�1�C2�C3�C6���o��A �ꍇ�ł��B
(ii)�̊m���́A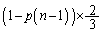
���A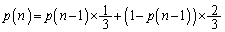
(�N) �@��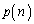 ��
��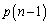 ��α�ƒu��������ƁA
��α�ƒu��������ƁA 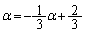 �@����A
�@����A�� 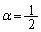 �@�|�A���A
�@�|�A���A ����āA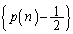 �́A�����F
�́A�����F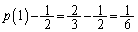 �C����F
�C����F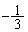 �����䐔���B
�����䐔���B
�� 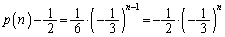 ��
�� 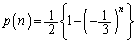 ......[��]
......[��]
(2)(�P) ���������100���āA1�̖ڂ����傤��k��(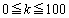 )�o��m��
)�o��m�� �́A
�́A
(�R) 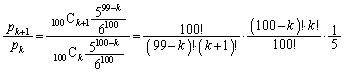
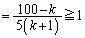 �@����B
�@����B�Ƃ���ƁA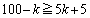
�� 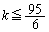 �B�ɂ����ē���������
�B�ɂ����ē���������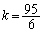 �̂Ƃ�(k�͎��R���Ȃ̂ŁA�����������Ƃ͋N����Ȃ�)�����ŁA
�̂Ƃ�(k�͎��R���Ȃ̂ŁA�����������Ƃ͋N����Ȃ�)�����ŁA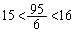 ������A
������A ������A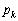 ���ő�ɂȂ�̂́A
���ő�ɂȂ�̂́A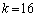 ......[��]�@�̂Ƃ��B
......[��]�@�̂Ƃ��B
(�T�V) ���������n���āA1�̖ڂ����傤��k��(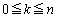 )�o��m��
)�o��m��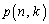 �́A
�́A �Ƃ���ƁA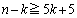
�� 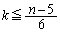 �@����C
�@����C
�C�̓��������藧��k�̒l�����݂��Ȃ��ꍇ�A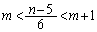 �Ƃ��āA
�Ƃ��āA ���̂Ƃ��́A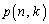 ���ő�ɂ���k�̒l��1��������܂���B
���ő�ɂ���k�̒l��1��������܂���B
�C�̓��������藧��k�̒l�����݂���ꍇ�A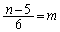 �Ƃ��āA
�Ƃ��āA ���̂Ƃ��́A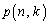 ���ő�ɂ���k�̒l�́A
���ő�ɂ���k�̒l�́A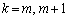 ��2����܂��B
��2����܂��B
�]���āA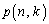 ���ő�ɂ���k�̒l��2���݂��邽�߂��K�v�\�������́A
���ő�ɂ���k�̒l��2���݂��邽�߂��K�v�\�������́A
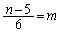 �C�܂�An��6�Ŋ������Ƃ��̗]�肪5�ƂȂ邱�Ƃł��B
�C�܂�An��6�Ŋ������Ƃ��̗]�肪5�ƂȂ邱�Ƃł��B
����āA(�T)��6�C(�V)��5 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B