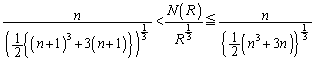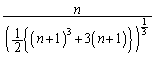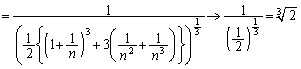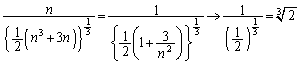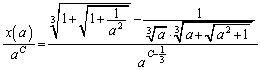�c�嗝�H���w'09�N[A4]
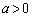 �Ƃ���B���̂Ƃ��A3��������
�Ƃ���B���̂Ƃ��A3��������
�͂�����̎�����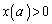 �����B���̐�R�ɑ��A
�����B���̐�R�ɑ��A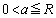 �͈̔͂�a�����Ƃ��A�Ή����������
�͈̔͂�a�����Ƃ��A�Ή����������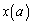 �������ƂȂ�悤��a�̌���
�������ƂȂ�悤��a�̌���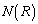 �Ƃ���B
�Ƃ���B
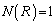 �ƂȂ�悤��R�͈̔͂��@�i�@
�ƂȂ�悤��R�͈̔͂��@�i�@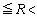 �@�j�@�ł���B
�@�j�@�ł���B
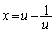 �Ƃ����A
�Ƃ����A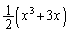 ��u�ŕ\�����@�k�@�ƂȂ�B���������āA
��u�ŕ\�����@�k�@�ƂȂ�B���������āA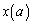 ��a���g���ĕ\����
��a���g���ĕ\����
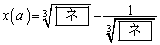 �@(
�@(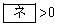 )
)
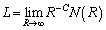 ���L���Ȑ��̒l�ƂȂ�̂�
���L���Ȑ��̒l�ƂȂ�̂�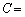 �@�m�@�̂Ƃ��ł���A���̂Ƃ�
�@�m�@�̂Ƃ��ł���A���̂Ƃ�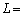 �@�n�@�ł���B
�@�n�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶���킩��ɂ����̂ł����A���������̖��̃|�C���g�Ȃ̂ŁA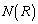 ���������������Ӗ�����̂��A�悭����ł������悤�ɂ��܂��傤�B�o��҂̈Ӑ}�����߂�A�e�ȗU���ɂȂ��Ă��邱�ƂɋC�Â���͂��ł��B
���������������Ӗ�����̂��A�悭����ł������悤�ɂ��܂��傤�B�o��҂̈Ӑ}�����߂�A�e�ȗU���ɂȂ��Ă��邱�ƂɋC�Â���͂��ł��B
�Ƃ����ƁA
���A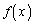 ���P���������ł��B
���P���������ł��B
�ƂȂ��Ă���̂ŁA�Ⴆ�A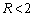 �Ƃ��āAa��
�Ƃ��āAa��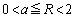 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A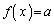 ����x��
����x��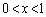 �ł�����x�͐����ɂȂ�Ȃ��̂ŁA
�ł�����x�͐����ɂȂ�Ȃ��̂ŁA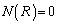 �ł��B
�ł��B
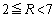 �Ƃ���ƁAa��
�Ƃ���ƁAa��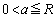 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A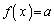 ��������x�́A
��������x�́A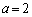 �̂Ƃ���
�̂Ƃ���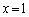 �݂̂ł����āA
�݂̂ł����āA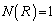 �ł��B
�ł��B
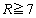 ���Ƃ���ƁAa��
���Ƃ���ƁAa��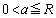 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A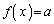 ��������x�́A
��������x�́A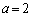 �̂Ƃ���
�̂Ƃ���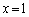 ��
��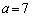 �̂Ƃ���
�̂Ƃ���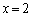 �̏��Ȃ��Ƃ�2����̂ŁA
�̏��Ȃ��Ƃ�2����̂ŁA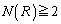 �ł��B
�ł��B
�]���āA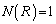 �ƂȂ�悤��R�͈̔͂�
�ƂȂ�悤��R�͈̔͂�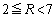 �ł��B
�ł��B
(�i) 2 ......[��]
(�j) 7 ......[��]
(�k) 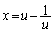 �Ƃ����ƁA
�Ƃ����ƁA 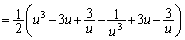
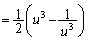 ......[��]
......[��]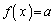 ���A
���A
�� 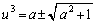 ��蕶���̎w��ɂ��
��蕶���̎w��ɂ��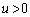 �ƂȂ�����Ƃ��āA
�ƂȂ�����Ƃ��āA (�m) a��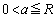 �͈̔͂œ������Ƃ��A
�͈̔͂œ������Ƃ��A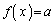 ����x�������ƂȂ�Ƃ��́ua�̌��v��
����x�������ƂȂ�Ƃ��́ua�̌��v��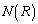 �Ȃ̂ł����A
�Ȃ̂ł����A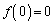 ��
��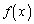 ���P���������ł��邱�Ƃ��l����ƁAa�̌���
���P���������ł��邱�Ƃ��l����ƁAa�̌���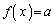 �����u����x�̌��v�Ɉ�v���Aa��
�����u����x�̌��v�Ɉ�v���Aa��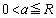 �͈̔͂œ������Ƃ���
�͈̔͂œ������Ƃ���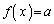 ��������x�̂����́u�ő�̐���n�v�ƈ�v���܂��B�܂�A
��������x�̂����́u�ő�̐���n�v�ƈ�v���܂��B�܂�A 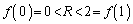 �̂Ƃ��A
�̂Ƃ��A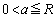 �͈̔͂�a��������
�͈̔͂�a��������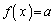 ��������x�͑��݂��Ȃ��̂ŁA
��������x�͑��݂��Ȃ��̂ŁA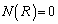
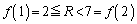 �̂Ƃ��A
�̂Ƃ��A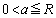 �͈̔͂�a��������
�͈̔͂�a��������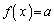 ��������x�́A
��������x�́A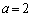 �̂Ƃ���
�̂Ƃ���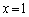 ��1����A
��1����A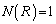
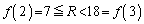 �̂Ƃ��A
�̂Ƃ��A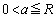 �͈̔͂�a��������
�͈̔͂�a��������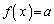 ��������x�́A
��������x�́A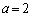 �̂Ƃ���
�̂Ƃ���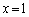 �ƁA
�ƁA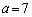 �̂Ƃ���
�̂Ƃ���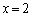 ��2����A
��2����A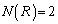
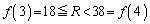 �̂Ƃ��A
�̂Ƃ��A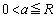 �͈̔͂�a��������
�͈̔͂�a��������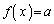 ��������x�́A
��������x�́A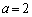 �̂Ƃ���
�̂Ƃ���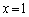 ��
��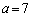 �̂Ƃ���
�̂Ƃ���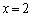 ��
��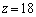 �̂Ƃ���
�̂Ƃ���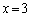 ��3����A
��3����A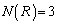
�Ƃ�����ɂȂ��Ă���̂ŁAn�����R���Ƃ��āA
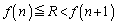 �̂Ƃ��A
�̂Ƃ��A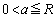 �͈̔͂�a��������
�͈̔͂�a��������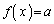 ��������x��
��������x��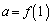 �̂Ƃ���
�̂Ƃ���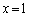 �C
�C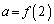 �̂Ƃ���
�̂Ƃ���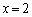 �C����C
�C����C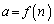 �̂Ƃ���
�̂Ƃ���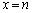 ��n����A
��n����A
�ƂȂ�܂��B����āA
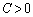 ���Ƃ��āA
���Ƃ��āA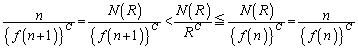 ��
�� 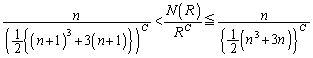 �@����A
�@����A���ӂ�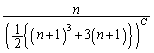 �ƉE�ӂ�
�ƉE�ӂ�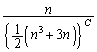 �́A
�́A
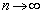 �Ƃ���ƁA
�Ƃ���ƁA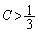 �ł�0�Ɏ������A
�ł�0�Ɏ������A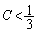 �ł͐��̖�����ɔ��U���܂�(����̋Ɍ����Q��)�B
�ł͐��̖�����ɔ��U���܂�(����̋Ɍ����Q��)�B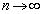 �̂Ƃ��A
�̂Ƃ��A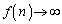 �C
�C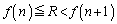 ���
���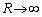 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA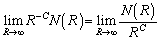 ���L���Ȑ��̒l�ƂȂ�̂́A
���L���Ȑ��̒l�ƂȂ�̂́A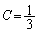 ......[��]�@�̂Ƃ��ł��B
......[��]�@�̂Ƃ��ł��B (�n) 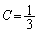 �̂Ƃ��A�A�́A
�̂Ƃ��A�A�́A 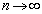 �Ƃ���ƁA
�Ƃ���ƁA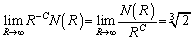 ......[��]
......[��]�ʉ��D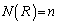 (n�F���R��)�̂Ƃ��A�@��
(n�F���R��)�̂Ƃ��A�@��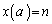 �Ƃ��āA
�Ƃ��āA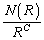 ��
�� �Ƃ��čl���A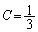 �̂Ƃ��ɂ̂�
�̂Ƃ��ɂ̂� �Ƃ��邱�Ƃ��ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 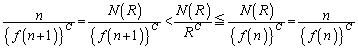
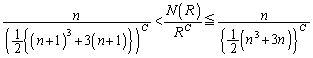 �@����A
�@����A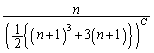 �ƉE�ӂ�
�ƉE�ӂ�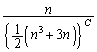 �́A
�́A