京都大学理系2002年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 数列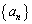
の初項
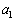から第n項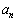
までの和を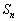
と表す。この数列が
を満たすとき、一般項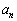
を求めよ。
[解答へ]
[2] 半径1の円周上に相異なる3点A，B，Cがある。
(1) 
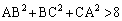ならば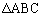
は鋭角三角形であることを示せ。 (2) 
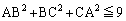が成立することを示せ。また、この等号が成立するのはどのような場合か。 [解答へ]
[3]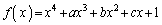 
は整数を係数とするxの4次式とする。4次方程式
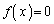の重複も込めた4つの解のうち、2つは整数で2つは虚数であるという。このときa，b，cの値を求めよ。
[解答へ]
[4](1)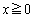 
で定義された関数
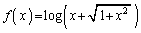について、導関数
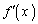を求めよ。
(2) 極方程式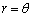
(
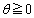)で定義される曲線の、
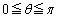の部分の長さを求めよ。
[解答へ]
[5] a，b，cを実数とする。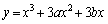
と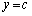
のグラフが相異なる3つの交点を持つという。このとき
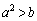が成立することを示し、さらにこれらの交点のx座標のすべては開区間
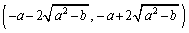に含まれていることを示せ。
[解答へ]
[6]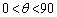 
とし、aは正の数とする。複素数平面上の点
，
，
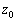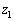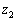，･･･ をつぎの条件(i)，(ii)を満たすように定める。
(i)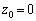 
, 
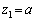
(ii)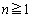 
のとき、点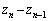
を原点のまわりに
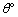回転すると点
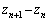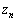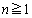に一致する。 このとき点
(
)が点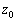
と一致するようなnが存在するための必要十分条件は、θ が有理数であることを示せ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
(
)