東京大学理系2003年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] a，b，cを実数とし、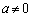
とする。2次関数
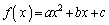が次の条件(A)，(B)を満たすとする。
このとき、積分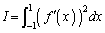
のとりうる値の範囲を求めよ。
[解答へ]
[2] Oを原点とする複素数平面上で6を表す点をA，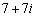
を表す点をBとする。ただし、iは虚数単位である。正の実数tに対し、
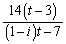を表す点Pをとる。
(1) 
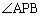を求めよ。 (2) 線分OPの長さが最大になるtを求めよ。
[解答へ]
[3] xyz空間において、平面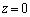
上の原点を中心とする半径2の円を底面とし、点
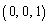を頂点とする円錐をAとする。
次に、平面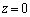
上の点
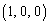を中心とする半径1の円をH，平面
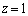上の点
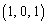を中心とする半径1の円をKとする。HとKを2つの底面とする円柱をBとする。円錐Aと円柱Bの共通部分をCとする。
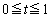を満たす実数tに対し、平面
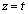によるCの切り口の面積を
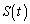とおく。
(2) Cの体積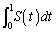
を求めよ。 [解答へ]
[4] 2次方程式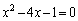
の2つの実数解のうち大きいものをα，小さいものをβ とする。
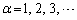に対し、
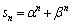とおく。(2)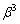 
以下の最大の整数を求めよ。 (3) 
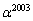以下の最大の整数の1の位の数を求めよ。 [解答へ]
[5] さいころをn回振り、第1回目から第n回目までに出たさいころの目の数n個の積を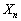
とする。
(1) 
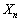が5で割り切れる確率を求めよ。 (2) 
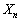が4で割り切れる確率を求めよ。 注意：さいころは1から6までの目が等確率で出るものとする。
[解答へ]
[6] 円周率が3.05より大きいことを証明せよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
を満たすすべてのxに対し、
とする。
のとき、
をθ で表せ。
，
，
を求めよ。また、
に対し、
を
と
で表せ。
が20で割り切れる確率を
とおく。
を求めよ。