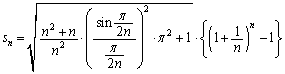東大理系数学'07年前期[2]
nを2以上の整数とする。平面上に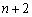 個の点O,
個の点O,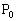 ,
,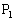 ,・・・,
,・・・,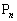 があり、次の2つの条件をみたしている。
があり、次の2つの条件をみたしている。
① 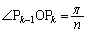 (
(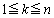 ),
),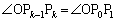 (
(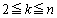 )② 線分
)② 線分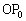 の長さは1,線分
の長さは1,線分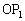 の長さは
の長さは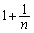 である。
である。 線分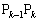 の長さを
の長さを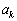 とし、
とし、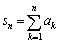 とおくとき、
とおくとき、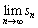 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
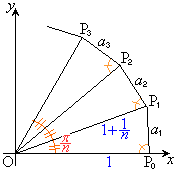 解答 この問題を落とすようでは、東京大学で学ぼうなどと思わないで欲しい、という問題です。
解答 この問題を落とすようでは、東京大学で学ぼうなどと思わないで欲しい、という問題です。
まず、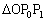 ,
,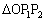 ,・・・,
,・・・,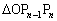 は、すべて、2角が等しい三角形で相似であることに気づく必要があります。となれば、相似比を考えて、
は、すべて、2角が等しい三角形で相似であることに気づく必要があります。となれば、相似比を考えて、
よって、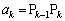 として、数列
として、数列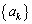 は等比数列であり、
は等比数列であり、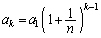
これで、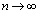 とするのですから、極限の公式:
とするのですから、極限の公式: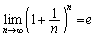 を使う問題なのだろう、というストーリーが見えてきます。
を使う問題なのだろう、というストーリーが見えてきます。
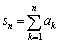 は、単に等比数列の和に過ぎません。公式を用いて、
は、単に等比数列の和に過ぎません。公式を用いて、
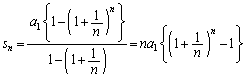 ・・・③
・・・③
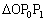 において、余弦定理より、
において、余弦定理より、
③に代入して、
∴ 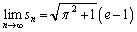 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 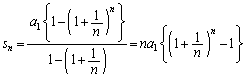 ・・・③
・・・③