東大文系数学'07年前期[2]
rは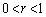 をみたす実数、nは2以上の整数とする。平面上に与えられた1つの円を、次の条件①,②をみたす2つの円で置き換える操作(P)を考える。
をみたす実数、nは2以上の整数とする。平面上に与えられた1つの円を、次の条件①,②をみたす2つの円で置き換える操作(P)を考える。
① 新しい2つの円の半径の比はr: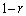 で、半径の和はもとの円の半径に等しい。
で、半径の和はもとの円の半径に等しい。 ② 新しい2つの円は互いに外接し、もとの円に内接する。
以下のようにして、平面上に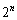 個の円を作る。
個の円を作る。
・最初に、平面上に半径1の円を描く。
・次に、この円に対して操作(P)を行い、2つの円を得る(これを1回目の操作という)。
・k回目の操作で得られた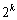 個の円のそれぞれについて、操作(P)を行い、
個の円のそれぞれについて、操作(P)を行い、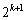 個の円を得る(
個の円を得る(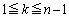 )。
)。 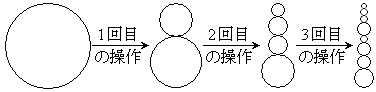 (1) n回目の操作で得られる
(1) n回目の操作で得られる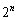 個の円の周の長さの和を求めよ。
個の円の周の長さの和を求めよ。(2) 2回目の操作で得られる4つの円の面積の和を求めよ。
(3) n回目の操作で得られる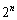 個の円の面積の和を求めよ。
個の円の面積の和を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 条件②の意味が不明です。重ならない、という程度のことなのでしょうか?
半径Rの円に操作(P)を施すと、半径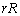 の円と半径
の円と半径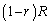 の円ができます。
の円ができます。
半径Rの円の円周の長さは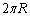 ,面積は
,面積は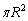 です。
です。
半径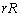 の円の円周の長さは
の円の円周の長さは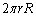 ,面積は
,面積は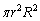 です。
です。
半径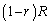 の円の円周の長さは
の円の円周の長さは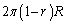 ,面積は
,面積は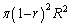 です。
です。
(1) 操作(P)の実行により、半径Rの円について、円周の長さの和は、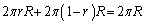 となり、変化しません。
となり、変化しません。 操作(P)実行前のすべての円について、円周の長さの和は変化せず、1回目の操作前の半径1の円周の長さは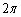 なので、n回目の操作で得られる
なので、n回目の操作で得られる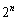 個の円の周の長さの和も
個の円の周の長さの和も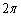 ......[答]
......[答]
(2) 操作(P)の実行により、半径Rの円について、円周の面積の和は、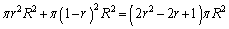 となり、
となり、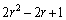 倍になります。
倍になります。 1回目の操作前の半径1の円の面積は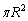 です。2回目の操作で得られる4つの円の面積の和は、
です。2回目の操作で得られる4つの円の面積の和は、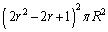 ......[答]
......[答]
(3) (2)より、n回目の操作で得られる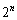 個の円の面積の和は、
個の円の面積の和は、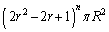 ......[答]
......[答]
注.要するに、n回操作後の円周の長さの和は、定数値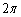 となる数列、n回操作後の面積の和は、初項
となる数列、n回操作後の面積の和は、初項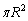 ,公比
,公比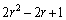 の等比数列、ということです。
の等比数列、ということです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。