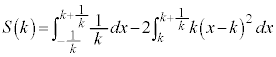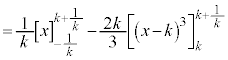���嗝�n���w'18�N�O��[3]
������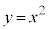 �̂���
�̂���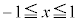 ���݂���������C�Ƃ���B���W���ʏ�̌��_O�Ɠ_A
���݂���������C�Ƃ���B���W���ʏ�̌��_O�Ɠ_A ���l����B
���l����B
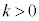 �������Ƃ���B�_P��C����A�_Q������OA����Ƃ��A
�������Ƃ���B�_P��C����A�_Q������OA����Ƃ��A
���݂����_R�������̈�̖ʐς�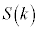 �Ƃ���B
�Ƃ���B
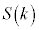 �����
�����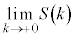 �C
�C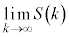 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�����̃O���t���������̂����嗝�n2011�N[6]���v���o�����܂��B�܂��͏퓅�I�ȉ�@�Ői�߂Ă݂܂����A�������ł͂��܂�̎�Ԃōl�����̂ł��B�{��ł́A�ǂ����ŏ퓅�I�ȉ�@��f�O���Ȃ��Ƒ�P�K�ɂȂ�܂��B����I�ɂ́A���_�o��ŁA�^���̈Ӗ����ȒP�ɐ�������ɗ��߂Đϕ��v�Z�Ɉڂ�ׂ��ŁA����Ȃ�債�����ł͂���܂���B
������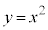 ��̓_P�̍��W��
��̓_P�̍��W��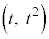 �C����OA��̓_Q��
�C����OA��̓_Q��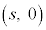 �Ƃ��܂��B
�Ƃ��܂��B �C
�C �ł��B
�ł��B
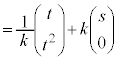 �@����@
�@����@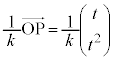 �̕����͕�����
�̕����͕�����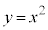 (2�������Q��)��
(2�������Q��)��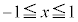 �̕��������_�𒆐S��
�̕��������_�𒆐S��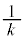 �{�ɏk�������}�`���܂��B
�{�ɏk�������}�`���܂��B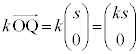 �ł����A
�ł����A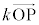 �ɂ����������Ƃ������Ƃ́A
�ɂ����������Ƃ������Ƃ́A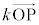 ��x����������
��x����������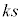 �������s�ړ����邱�Ƃ��Ӗ����܂��B
�������s�ړ����邱�Ƃ��Ӗ����܂��B
 �����ŁA���̕��͋C�����ނ��߂ɁA
�����ŁA���̕��͋C�����ނ��߂ɁA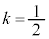 �̏ꍇ�A
�̏ꍇ�A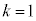 �̏ꍇ�A
�̏ꍇ�A �̏ꍇ�ɂ��āAs��
�̏ꍇ�ɂ��āAs��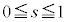 �͈̔͂ŁA0����1�܂�
�͈̔͂ŁA0����1�܂�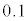 ���������āA
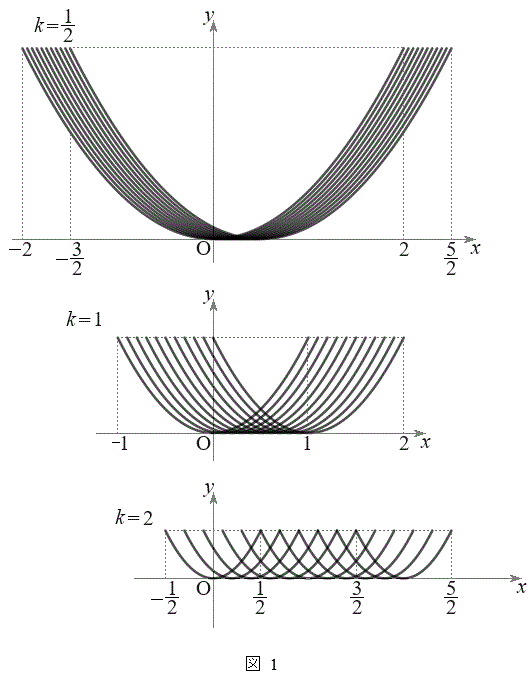
���������āA �̕��������ǂ��Ȃ邩��}1�Ɏ����܂��B�������ł́A
�̕��������ǂ��Ȃ邩��}1�Ɏ����܂��B�������ł́A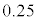 �����������炢�ŏ[���ɗ̈悪�ǂ�Ȃ��̂����߂�͂��ł��B
�����������炢�ŏ[���ɗ̈悪�ǂ�Ȃ��̂����߂�͂��ł��B
�����������ł́Ax�Cy�̂ǂ��炩���Œ肵�āA�������ǂ̂悤�Ȕ͈͂̒l���Ƃ邩���ׂ�̂��퓅��i�ł����A�����ł́Ax���Œ肵��y�̎�肤��l�͈̔͂��l���Ă݂܂��B
�@���A
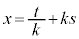 �C
�C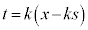 �@����A
�@����A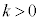 �C
�C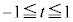 ���A
���A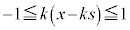 �C
�C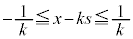
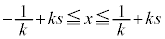
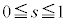 �Ȃ̂�
�Ȃ̂�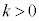 ���A
���A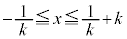 �@����B
�@����B
�@�C�A���A
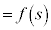 �@����C�@�Ƃ����܂��B
�@����C�@�Ƃ����܂��B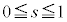 �ɂ�����ő�ŏ�(2�����̍ő�E�ŏ����Q��)���l���邱�ƂɂȂ�܂����A�����ŁA
�ɂ�����ő�ŏ�(2�����̍ő�E�ŏ����Q��)���l���邱�ƂɂȂ�܂����A�����ŁA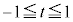 ���A
���A
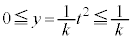 �@����D
�@����D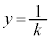 �C�܂�
�C�܂�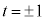 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A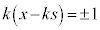 �C
�C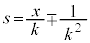 (��������)
(��������)
����s�ɂ��āA�������}�C�i�X��s��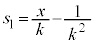 �C�������v���X��s��
�C�������v���X��s��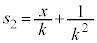 �Ƃ��܂��B�@����E
�Ƃ��܂��B�@����E
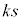 ����x�������ɕ��s�ړ������������̑��ݔ͈͂��l����ƁA
����x�������ɕ��s�ړ������������̑��ݔ͈͂��l����ƁA
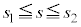 �@����F
�@����F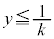 �ɒ��ӂ��Ă��������B
�ɒ��ӂ��Ă��������B
�Ƃ���ŁA2�����C�̎��̈ʒu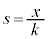 ��
��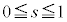 �͈̔͂Ƃ̈ʒu�W�A�F��
�͈̔͂Ƃ̈ʒu�W�A�F��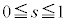 �Ƃ̊W���l���āA�B������ɏꍇ�������čl����K�v������܂��B
�Ƃ̊W���l���āA�B������ɏꍇ�������čl����K�v������܂��B
�܂��A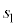 ��
��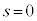 �Ƃ̑召�ׂ܂��A�E��
�Ƃ̑召�ׂ܂��A�E��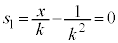 �Ƃ����
�Ƃ����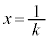 �Ȃ̂ŁA
�Ȃ̂ŁA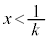 ��
��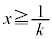 �ŕ����܂��B
�ŕ����܂��B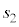 ��
��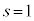 �Ƃ̑召�ׂ�ƁA�E��
�Ƃ̑召�ׂ�ƁA�E��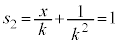 �Ƃ����
�Ƃ����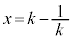 �Ȃ̂ŁA
�Ȃ̂ŁA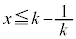 ��
��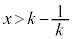 �ŕ����܂��B
�ŕ����܂��B
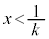 �̂Ƃ�
�̂Ƃ�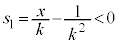 �C
�C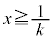 �̂Ƃ�
�̂Ƃ�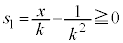 �ł��B
�ł��B
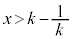 �̂Ƃ�
�̂Ƃ�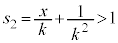 �C
�C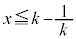 �̂Ƃ�
�̂Ƃ�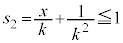 �ł��B
�ł��B
�ȏ���B���l�����Đ�������ƁA
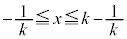 (
(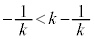 �ł�)�̂Ƃ�
�ł�)�̂Ƃ�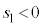 �C
�C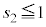 �@����G
�@����G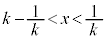 (
(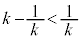 �ł�)�̂Ƃ��A
�ł�)�̂Ƃ��A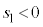 �C
�C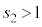 �@����H
�@����H
�܂�s�͈̔�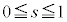 �́A�F��
�́A�F��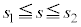 �̓����ɂ���܂��B
�̓����ɂ���܂��B
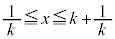 �̂Ƃ�
�̂Ƃ�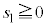 �C
�C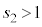 �@����I
�@����I
�܂��A�C�̎��̈ʒu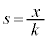 ��s�͈̔�
��s�͈̔�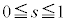 �̒����ɂ���Ƃ�
�̒����ɂ���Ƃ�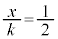 �Ƃ���
�Ƃ���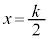 �Cs�͈̔�
�Cs�͈̔�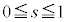 �̉E�[�ɂ���Ƃ�
�̉E�[�ɂ���Ƃ�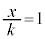 �Ƃ���
�Ƃ���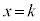 �C����āA�C�̎��̈ʒu
�C����āA�C�̎��̈ʒu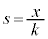 �́A
�́A
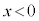 �̂Ƃ�
�̂Ƃ�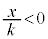 ���As�͈̔�
���As�͈̔�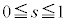 �̍����ɂ���܂��B
�̍����ɂ���܂��B
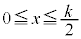 �̂Ƃ�
�̂Ƃ�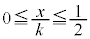 ���As�͈̔�
���As�͈̔�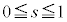 ���̒������獶���ɂ���܂��B
���̒������獶���ɂ���܂��B
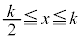 �̂Ƃ�
�̂Ƃ�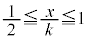 ���As�͈̔�
���As�͈̔�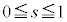 ���̒�������E���ɂ���܂��B
���̒�������E���ɂ���܂��B
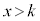 �̂Ƃ�
�̂Ƃ�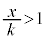 ���As�͈̔�
���As�͈̔�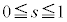 �̉E���ɂ���܂��B
�̉E���ɂ���܂��B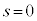 �̂Ƃ��̕�����(
�̂Ƃ��̕�����(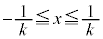 �͈̔͂ɂ���)��
�͈̔͂ɂ���)�� �̂Ƃ��̕�����(
�̂Ƃ��̕�����(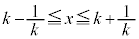 �͈̔͂ɂ���)�����L�_�����ꍇ�Ǝ����Ȃ��ꍇ�ƂŁA�Ⴂ�����邱�Ƃ��킩��܂��B���L�_�����Ƃ��A
�͈̔͂ɂ���)�����L�_�����ꍇ�Ǝ����Ȃ��ꍇ�ƂŁA�Ⴂ�����邱�Ƃ��킩��܂��B���L�_�����Ƃ��A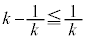 �C�܂�A
�C�܂�A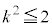 �C�܂�
�C�܂�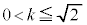 �ł��B
�ł��B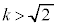 �̂Ƃ��͋��L�_�������܂���B
�̂Ƃ��͋��L�_�������܂���B
����ɁA�G�C�H�̏ꍇ�����ƁA���ʒu�ɂ��ꍇ����������ƁA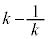 �̐����ɂ���Ă�������K�v������܂��B
�̐����ɂ���Ă�������K�v������܂��B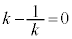 �Ƃ����
�Ƃ����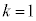 �ł��B
�ł��B
����āA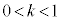 �C
�C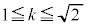 �C
�C �ŕ����čl����K�v������܂��B
�ŕ����čl����K�v������܂��B
 �E
�E �̂Ƃ��A
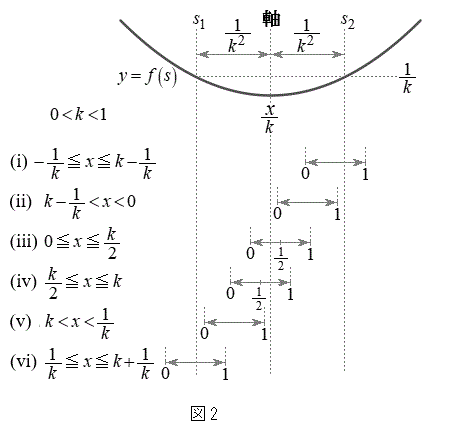
�̂Ƃ��A �ł��邱�Ƃɒ��ӂ��Đ}2�̂悤��x�͈̔͂��A
�ł��邱�Ƃɒ��ӂ��Đ}2�̂悤��x�͈̔͂��A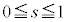 �ɂ�����C�̍ő�ŏ����l���܂��B
�ɂ�����C�̍ő�ŏ����l���܂��B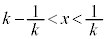 �̂Ƃ��ɂ́A�H���A
�̂Ƃ��ɂ́A�H���A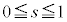 �͇F�͈͓̔��ɂ���܂��B
�͇F�͈͓̔��ɂ���܂��B(i) 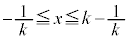 �̂Ƃ��F�D�C�G���C�̍ő�l��
�̂Ƃ��F�D�C�G���C�̍ő�l��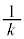 (�F���
(�F���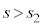 �ɂ͂Ȃ�܂���)�C�C�̎���
�ɂ͂Ȃ�܂���)�C�C�̎���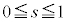 �̍����ŁA
�̍����ŁA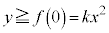 �C�܂�
�C�܂�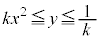
(ii) 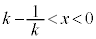 �̂Ƃ��F�C�̎���
�̂Ƃ��F�C�̎���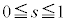 ��荶���ɂ����āC�C�́A
��荶���ɂ����āC�C�́A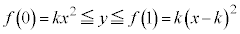
(iii) 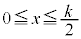 �̂Ƃ��F�C�̎���
�̂Ƃ��F�C�̎���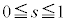 ���̒������獶����
���̒������獶����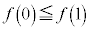 �C�C�́A
�C�C�́A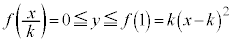
(iv) 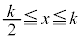 �̂Ƃ��F�C�̎���
�̂Ƃ��F�C�̎���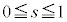 ���̒�������E����
���̒�������E����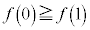 �C�C�́A
�C�C�́A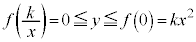
(v) 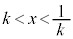 �̂Ƃ��F�C�̎���
�̂Ƃ��F�C�̎���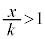 ���
���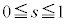 ���E���ɂ����āA�C�́A
���E���ɂ����āA�C�́A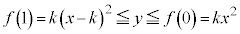
(vi) 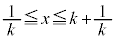 �̂Ƃ��F�D�C�I���C�̍ő�l��
�̂Ƃ��F�D�C�I���C�̍ő�l��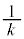 (�F���
(�F���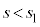 �ɂ͂Ȃ�܂���)�C�C�̎���
�ɂ͂Ȃ�܂���)�C�C�̎���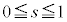 ���E���ŁA
���E���ŁA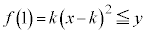 �C�܂�A
�C�܂�A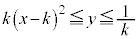
�E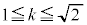 �̂Ƃ��A�B���l�����A
�̂Ƃ��A�B���l�����A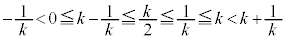 �ł��邱�Ƃɒ��ӂ���x�͈̔͂��A
�ł��邱�Ƃɒ��ӂ���x�͈̔͂��A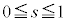 �ɂ�����C�̍ő�ŏ����l���܂��B
�ɂ�����C�̍ő�ŏ����l���܂��B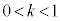 �̂Ƃ��Əꍇ�������قȂ�܂��B�܂��A
�̂Ƃ��Əꍇ�������قȂ�܂��B�܂��A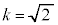 �̂Ƃ�
�̂Ƃ�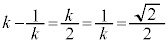 �ƂȂ�A�ȉ���(iii)��(iv)�̏ꍇ�������Ȃ��Ȃ邱�Ƃɂ����ӂ��Ă��������B
�ƂȂ�A�ȉ���(iii)��(iv)�̏ꍇ�������Ȃ��Ȃ邱�Ƃɂ����ӂ��Ă��������B (i) 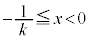 �̂Ƃ��F�D���C�̍ő�l��
�̂Ƃ��F�D���C�̍ő�l��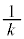 �C�C�̎���
�C�C�̎���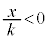 ���
���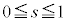 ��荶���ɂ����āA
��荶���ɂ����āA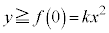 �C�܂�
�C�܂�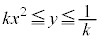
(ii) 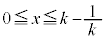 �̂Ƃ��F�D���C�̍ő�l��
�̂Ƃ��F�D���C�̍ő�l��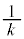 �C�C�̎���
�C�C�̎���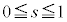 �̒��ɂ���A
�̒��ɂ���A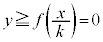 �C�܂�A
�C�܂�A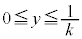
(iii) 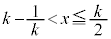 �̂Ƃ��F�C�̎���
�̂Ƃ��F�C�̎���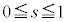 ���̒������獶����
���̒������獶����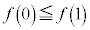 �C�C�́A
�C�C�́A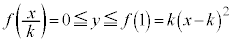
(iv) 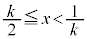 �̂Ƃ��F�C�̎���
�̂Ƃ��F�C�̎���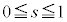 ���̒�������E����
���̒�������E����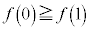 �C�C�́A
�C�C�́A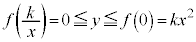
(v) 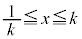 �̂Ƃ��F�D���C�̍ő�l��
�̂Ƃ��F�D���C�̍ő�l��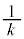 �C�C�̎���
�C�C�̎���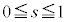 �̒��ɂ���A
�̒��ɂ���A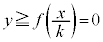 �C�܂�A
�C�܂�A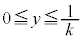
(iv) 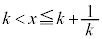 �̂Ƃ��F�D���C�̍ő�l��
�̂Ƃ��F�D���C�̍ő�l��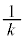 �C�C�̎���
�C�C�̎���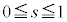 ���E���ɂ����āA
���E���ɂ����āA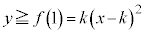 �C�܂�
�C�܂�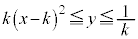
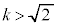 �ƂȂ�A
�ƂȂ�A �̂Ƃ��̕�������
�̂Ƃ��̕������� �̂Ƃ��̕����������L�_�������Ȃ��ꍇ�A
�̂Ƃ��̕����������L�_�������Ȃ��ꍇ�A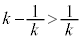 �ł����āA
�ł����āA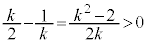 �C
�C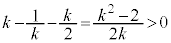 ���A
���A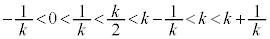 �ƂȂ�A
�ƂȂ�A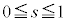 �ɂ�����C�̍ő�ŏ����l����ƁA
�ɂ�����C�̍ő�ŏ����l����ƁA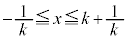 �̑S�͈͂ɂ����āA
�̑S�͈͂ɂ����āA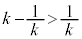 �ƇD���A
�ƇD���A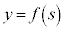 �̍ő�l��
�̍ő�l��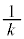 �ł��B
�ł��B
(i) 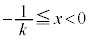 �̂Ƃ��A
�̂Ƃ��A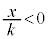 ���C�̎���
���C�̎���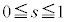 ���������ŁA
���������ŁA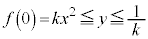
(iii) 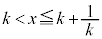 �̂Ƃ��A�C�̎���
�̂Ƃ��A�C�̎���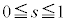 �����E���ŁA
�����E���ŁA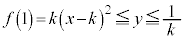
����ŗ̈�����߂邱�Ƃ��ł��܂����A�ȏ�̂悤�Ȃ��Ƃ��������ł���Ă�����ƂĂ����Ԃ�����܂���B�{��̏ꍇ�A�ʐς��Ă��邾���ŁA�̈�����߂�A�Ƃ������ł͂Ȃ��A�}1�̂悤�Ȑ}��`���Ă݂�A�ʐς����߂�̈悭�炢�Ȃ�[���c���ł��܂��B���i�̂��߂ɂ́A�{��ł͌��_�o��ŁA�ȉ��ɏ����悤�ɁA���s�ړ��̏��y������������x�ɗ��߂Ėʐόv�Z�Ɉڂ�ׂ��ł��B
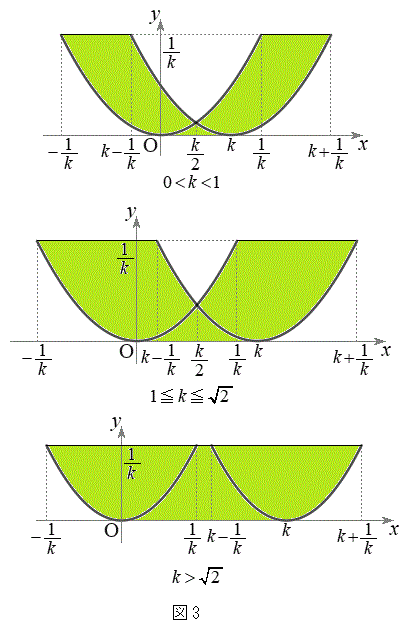 �_R�������Ăł���̈�́A������
�_R�������Ăł���̈�́A������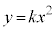 ��
�� �̕������Ax����������k�������s�ړ�������Ƃ��ɒʉ߂���̈�ł��B������
�̕������Ax����������k�������s�ړ�������Ƃ��ɒʉ߂���̈�ł��B������ �ł́A
�ł́A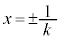 �̂Ƃ���
�̂Ƃ���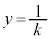 �ł���A
�ł���A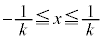 �Ƃ����͈͂�x����������k�������s�ړ�������ƁA
�Ƃ����͈͂�x����������k�������s�ړ�������ƁA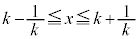 �Ƃ����͈͂Ɉڂ�܂��B
�Ƃ����͈͂Ɉڂ�܂��B
�܂��A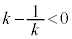 �̂Ƃ�
�̂Ƃ�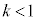 �C
�C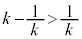 �̂Ƃ�
�̂Ƃ�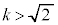 �ł��B����āA�_R�������Ăł���̈���A
�ł��B����āA�_R�������Ăł���̈���A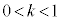 �̂Ƃ��A
�̂Ƃ��A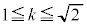 �̂Ƃ��A
�̂Ƃ��A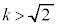 �̂Ƃ���3�ʂ�ɕ����Đ}������Ɛ}3�̂悤�ɂȂ�܂��B�̈�͂�������A
�̂Ƃ���3�ʂ�ɕ����Đ}������Ɛ}3�̂悤�ɂȂ�܂��B�̈�͂�������A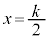 �Ɋւ��đΏ̂ł��邱�Ƃɒ��ӂ���ƁA�̈�̖ʐ�
�Ɋւ��đΏ̂ł��邱�Ƃɒ��ӂ���ƁA�̈�̖ʐ�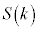 �͈ȉ��̂悤�ɂȂ�܂��B�ʐς����߂��ϕ��̎��́A
�͈ȉ��̂悤�ɂȂ�܂��B�ʐς����߂��ϕ��̎��́A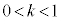 �̏ꍇ��
�̏ꍇ��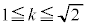 �̏ꍇ�Ƃœ����ł��B
�̏ꍇ�Ƃœ����ł��B
�E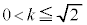 �̂Ƃ��A
�̂Ƃ��A
�E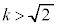 �̂Ƃ��A
�̂Ƃ��A
�ȏ���A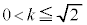 �̂Ƃ�
�̂Ƃ�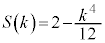 �C
�C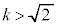 �̂Ƃ�
�̂Ƃ�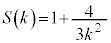 �C
�C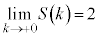 �C
�C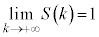 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@����@
�@����@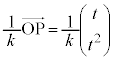 �̕����͕�����
�̕����͕�����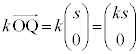 �ł����A
�ł����A