���嗝�H���w'05�N[2]
�~�����m�̓_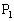 �C
�C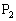 �C����C
�C����C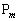 �����̏��ɔz�u����A�e�_
�����̏��ɔz�u����A�e�_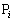 �Ɉ�̎���
�Ɉ�̎���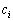 ���^�����Ă���(
���^��������(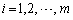 )�B�������A
)�B�������A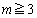 �Ƃ���B����ɁA
�Ƃ���B����ɁA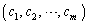 �͏���
�͏���
(��)�@�e�_�̒l�́A�אڂ���2�_�̒l�̘a�ɓ�����
�����B���̂Ƃ��A�ȉ��̖�ɓ�����B
(1) 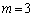 �̂Ƃ��A
�̂Ƃ��A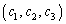 �̒l�����߂�B
�̒l�����߂�B (2) 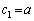 �C
�C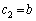 �Ƃ����Ƃ��A
�Ƃ����Ƃ��A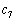 ��a�Cb�ŕ\���B�������A
��a�Cb�ŕ\���B�������A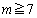 �Ƃ���B
�Ƃ���B (3) ����(��)���݂����A����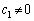 �ƂȂ�
�ƂȂ�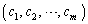 �����݂���̂�m���ǂ̂悤�Ȏ��R���̂Ƃ����Bm���������ׂ��K�v�\�����������߁A���̗��R���ȒP�ɏq�ׂ�B
�����݂���̂�m���ǂ̂悤�Ȏ��R���̂Ƃ����Bm���������ׂ��K�v�\�����������߁A���̗��R���ȒP�ɏq�ׂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@6�����ƂɌJ��Ԃ���������ł��邱�Ƃ����j��悢�A�Ƃ������ł��B
������A�����ĉ����ƁA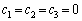
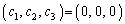 ......[��]
......[��]
(2) ����(��)�́A�ȉ��̂悤�ɗ����ł��܂��B
������A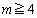 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A �� 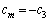
�� 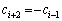 (
(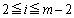 ) ����A
) ����A
�A�ɂ�����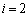 �Ƃ��āA
�Ƃ��āA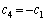
�A�ɂ�����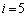 �Ƃ��āA
�Ƃ��āA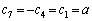 ......[��]���̐ݖ�̉Ƃ��ẮA����ŏI���ł����A(3)�̂��߂ɂ����������ׂ܂��B
......[��]���̐ݖ�̉Ƃ��ẮA����ŏI���ł����A(3)�̂��߂ɂ����������ׂ܂��B
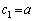 �C
�C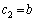
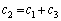 ���A
���A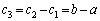
��L�̂悤�ɁA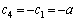
�A�ɂ�����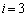 �Ƃ��āA
�Ƃ��āA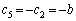
�A�ɂ�����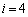 �Ƃ��āA
�Ƃ��āA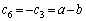
����ŁA����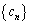 �́A
�́A ��6�̐����J��Ԃ���A�Ō��1�g���A���傤�ǖ����̂Ƃ��납�A���邢�͓r���Ő��悤�Ȑ��Ƃ킩��܂��B
(3) ����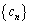 ��6�̐����J��Ԃ���鐔�Ƃ������Ƃ́A����m��6�̔{���ł���A
��6�̐����J��Ԃ���鐔�Ƃ������Ƃ́A����m��6�̔{���ł���A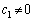 �ɂł������ł��B
�ɂł������ł��B 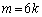 (k�F���R��)�̂Ƃ��A
(k�F���R��)�̂Ƃ��A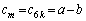 �ƂȂ�܂����A
�ƂȂ�܂����A
�Ⴆ�A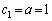 �C
�C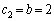 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA1������Ă����Ō�̕����ł́A
�ł����āA����(��)�͖�������Ă��܂��B
����m��6�̔{���łȂ��Ƃ��A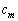 �́A
�́A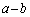 �ȊO�ł����āAa�Cb�C
�ȊO�ł����āAa�Cb�C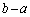 �C
�C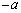 �C
�C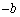 �̂ǂꂩ�ł��B
�̂ǂꂩ�ł��B
�ȉ��Ak��0�ȏ�̐������Ƃ��āAm��6�Ŋ������]��ŏꍇ�������A�e�ꍇ�ɂ��āA�@�́A 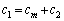 �C
�C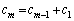
���݂������悤��a�Cb�͂ǂ�Ȑ����A���ׂ܂��B
�ȏ���A����(��)���݂����A����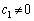 �ƂȂ�
�ƂȂ�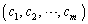 �����݂���̂�m��6�̔{���̂Ƃ��Ɍ����邱�Ƃ��킩��܂��B
�����݂���̂�m��6�̔{���̂Ƃ��Ɍ����邱�Ƃ��킩��܂��B
���߂�K�v�\�������́A���R��m���u6�̔{���ł��邱�Ɓv ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B