早稲田大学理工学部2006年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 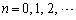 に対して、関数
に対して、関数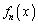 を
を
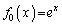 ,
,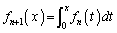
(1) 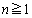 にたいして
にたいして を示せ。
(2) 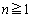 とする。
とする。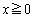 に対して、不等式
に対して、不等式 を示せ。
(3) 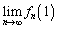 を求めよ。
を求めよ。 [解答へ]
[2] 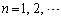 に対してxの整式
に対してxの整式
を考える。以下の問に答えよ。
(1) 3次方程式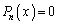 の正の実数解はただ1つであることを示せ。
の正の実数解はただ1つであることを示せ。 (2) tが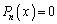 の解であるとき、
の解であるとき、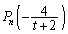 を求めよ。
を求めよ。 (3) 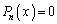 の正の実数解を
の正の実数解を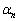 とするとき、
とするとき、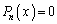 の最小の実数解
の最小の実数解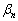 を
を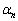 で表せ。さらに、
で表せ。さらに、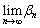 を求めよ。
を求めよ。 [解答へ]
[3] 数列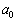 ,
,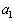 ,
,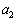 ,・・・ は条件
,・・・ は条件
を満たすとする。以下の問に答えよ。
(2) 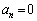 を満たすnがあることを示せ。
を満たすnがあることを示せ。 [解答へ]
[4] xy平面において原点Oから出発する動点Pが確率p (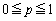 )でx軸の正方向と
)でx軸の正方向と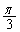 の角度をなす方向に、確率
の角度をなす方向に、確率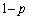 でx軸の正方向と
でx軸の正方向と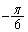 の角度をなす方向に進み、どちらの場合もOからの距離が1である点に到達するものとする。この到達点をAとする。さらに動点Pについて以下の2通りの移動(イ),(ロ)を考える。
の角度をなす方向に進み、どちらの場合もOからの距離が1である点に到達するものとする。この到達点をAとする。さらに動点Pについて以下の2通りの移動(イ),(ロ)を考える。
(イ) 動点Pが点Aから出発し確率pでx軸の正方向と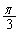 の角度をなす方向に、確率
の角度をなす方向に、確率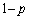 でx軸の正方向と
でx軸の正方向と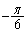 の角度をなす方向に進み、どちらの場合もAからの距離が1である点に到達するものとする。この到達点をBとする。
の角度をなす方向に進み、どちらの場合もAからの距離が1である点に到達するものとする。この到達点をBとする。 (ロ) 動点Pが点Aから出発し確率pで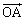 と
と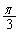 の角度をなす方向に、確率
の角度をなす方向に、確率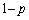 で
で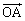 と
と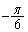 の角度をなす方向に進み、どちらの場合もAからの距離が1である点に到達するものとする。この到達点をCとする。
の角度をなす方向に進み、どちらの場合もAからの距離が1である点に到達するものとする。この到達点をCとする。 以下の問に答えよ。
(1) 線分OBの長さの2乗の期待値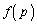 を求めよ。
を求めよ。 (2) 線分OCの長さの2乗の期待値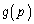 を求めよ。
を求めよ。 (3) 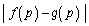 の最大値を求めよ。
の最大値を求めよ。 [解答へ]
[5] 動点Pはx軸の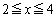 の部分、動点Qはy軸の
の部分、動点Qはy軸の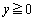 の部分を
の部分を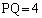 を満たしながら動く。このとき線分PQが動いてできる領域をFとする。またOは原点とし、
を満たしながら動く。このとき線分PQが動いてできる領域をFとする。またOは原点とし、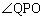 をαとする。
をαとする。
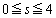 を満たすsを固定したとき、点
を満たすsを固定したとき、点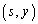 がFに属するようなyの最大値をtとし、線分PQが点
がFに属するようなyの最大値をtとし、線分PQが点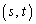 を通るときのαの値をθ とする。以下の問に答えよ。
を通るときのαの値をθ とする。以下の問に答えよ。
(1) 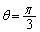 が成り立つsの範囲を求めよ。
が成り立つsの範囲を求めよ。 (2) sが(1)で求めた範囲に属さないときs,tをθ で表せ。
(3) Fの面積を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。