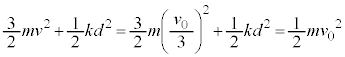���n�ɂ�����G�l���M�[�ۑ�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���n�ɂ����Ă��͊w�I�G�l���M�[�ۑ������l���邱�Ƃ��ł��܂��B�ȉ��ł́A����̗�ŁA���n�ɂ��������������d�����l���邱�Ƃɂ��A�͊w�I�G�l���M�[�ۑ���K�p�ł��邱�Ƃ��m���߂܂��B
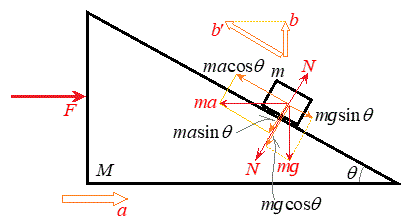 [1]�@�ŏ��̗�́A�����͂����ŁA���Ή����x(���n�Ō��������x)�����̏ꍇ�ł��B
[1]�@�ŏ��̗�́A�����͂����ŁA���Ή����x(���n�Ō��������x)�����̏ꍇ�ł��B�E�}�̂悤�ɁA�����ʂƊpθ���Ȃ�����M�̉��Ζʏ�Ɏ���m�̕��̂��u����Ă��āA���̂ƎΖʂ̊Ԃɖ��C�͂Ȃ����̂Ƃ���B���̏�ԂŎ���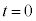 �Ȍ�A�ΖʂɎΖʂ����������ɐ��������̗�F�������āA�ΖʂɈ������xa��^����ƁA�Ζʏ�Ō��đ傫��
�Ȍ�A�ΖʂɎΖʂ����������ɐ��������̗�F�������āA�ΖʂɈ������xa��^����ƁA�Ζʏ�Ō��đ傫��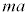 �̊����͂���������B
�̊����͂���������B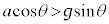 �̂Ƃ��A���͎̂Ζʏ������Ă����B
�̂Ƃ��A���͎̂Ζʏ������Ă����B
�Ζʏ�Ō����Ζʂɉ��������̕��̂��^���������́A�Ζʂ��������̕��̂̉����x��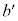 �Ƃ��āA
�Ƃ��āA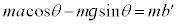
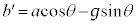 �@����@
�@����@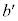 �͈��ŁA�Ζʏ�Ō��ĕ��̂̉^�����������x�^���ł��B
�͈��ŁA�Ζʏ�Ō��ĕ��̂̉^�����������x�^���ł��B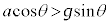 �̂Ƃ��A����t �̊ԂɁA�Ζʂ���镨�̂̑��x��
�̂Ƃ��A����t �̊ԂɁA�Ζʂ���镨�̂̑��x��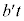 �ƂȂ�A���͎̂Ζʏ��
�ƂȂ�A���͎̂Ζʏ��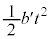 �������܂��B���������̕ψʂ�
�������܂��B���������̕ψʂ�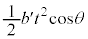 �ł��B���͉̂���������
�ł��B���͉̂���������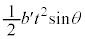 ���A���̂͏d�͂��ʒu�G�l���M�[
���A���̂͏d�͂��ʒu�G�l���M�[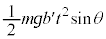 ���^���G�l���M�[
���^���G�l���M�[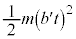 ��̂ł����A�����̃G�l���M�[���������Ă�����͉̂��ł��傤���H
��̂ł����A�����̃G�l���M�[���������Ă�����͉̂��ł��傤���H
�@��p����ƁA���̂�����͊w�I�G�l���M�[�́A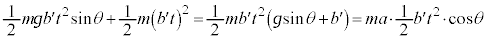 �@����A
�@����A�A�E�ӂ́A�ړ������Ɗpθ���Ȃ���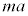 ������
������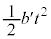 �����������Ƃɂ���Ĕ��������d���ƌ��邱�Ƃ��ł��܂��B�܂�A����́A������
�����������Ƃɂ���Ĕ��������d���ƌ��邱�Ƃ��ł��܂��B�܂�A����́A������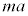 �̂����d���ł���A�A�͎Ζʏ�Ō����͊w�I�G�l���M�[�ۑ��̎��ƌ��邱�Ƃ��ł��܂��B
�̂����d���ł���A�A�͎Ζʏ�Ō����͊w�I�G�l���M�[�ۑ��̎��ƌ��邱�Ƃ��ł��܂��B
���̏�����Ō��čl���Ă݂܂��B
�Ζʂƕ��̂̊Ԃɂ������R��N�������̂ŁA
�����猩���Ζʂ̉^���������́A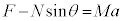 �@����B
�@����B
�����猩�����̂̉��������̉^���������́A���̂̉����x�̉���������b�Ƃ��āA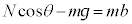 �@����C
�@����C
����Ō��Ă��A�Ζʏ�Ō��Ă��A���̂̉��������̉����x�͈�v���܂��B�܂�A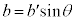 �@����D
�@����D
�D���C�ɑ������ƁA�@���A �� 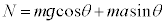 (����́A�Ζʂɐ����ȕ������͂̂荇�����Ӗ����܂��B�܂�D�����藧�Ƃ��A���͎̂Ζʂɉ��������ɂ̂݉^�����܂�)�B���A
(����́A�Ζʂɐ����ȕ������͂̂荇�����Ӗ����܂��B�܂�D�����藧�Ƃ��A���͎̂Ζʂɉ��������ɂ̂݉^�����܂�)�B���A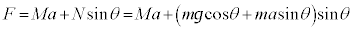
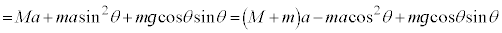
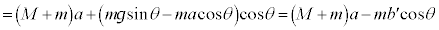 �@(�� �@)�@����E
�@(�� �@)�@����E
����Ō��Ă��A�Ζʏ�Ō��Ă����������̏㏸�����͓������A����t �ɂ����āA�d�͂̈ʒu�G�l���M�[�̑������́A 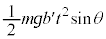 �@����F
�@����F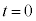 �ɂ�����͊w�I�G�l���M�[��0�ł��B�Ζʂ͈������x�ʼn^������̂ŁA����t �ɂ�����^���G�l���M�[�́A
�ɂ�����͊w�I�G�l���M�[��0�ł��B�Ζʂ͈������x�ʼn^������̂ŁA����t �ɂ�����^���G�l���M�[�́A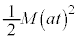 �ł��B
�ł��B
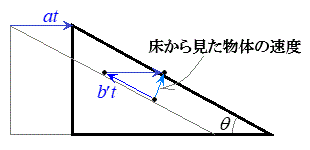 �Ζʏ�Ō������̂��Ζʂ���鑬�x��
�Ζʏ�Ō������̂��Ζʂ���鑬�x��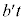 �ł����A�Ζʂ����x
�ł����A�Ζʂ����x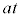 �Ő��������ɓ����̂ŁA�E�}�̂悤�ɁA�����猩�����̂̑��x�̑傫��
�Ő��������ɓ����̂ŁA�E�}�̂悤�ɁA�����猩�����̂̑��x�̑傫��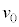 ��2��́A�]���藝���A
��2��́A�]���藝���A����āA����t �ɂ����镨�̂̉^���G�l���M�[�́A
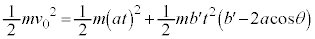 �@����G
�@����G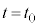 �ɂ����鏰���猩���ʒu�G�l���M�[�͇F�ł����āA�����猩���͊w�I�G�l���M�[�́A
�ɂ����鏰���猩���ʒu�G�l���M�[�͇F�ł����āA�����猩���͊w�I�G�l���M�[�́A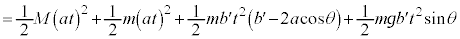 �@(�� �G)
�@(�� �G)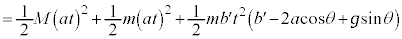
�@���A
�܂菰���猩�ăG�l���M�[�ۑ����l����ƁA�O�������������F���A�Ζʂ��ړ�����������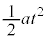 �����������Ƃ����d���Ɉ�v���܂��B�d�͂̎d���́A�d�͂̈ʒu�G�l���M�[�Ƃ��čl���Ă���̂ŁA�n�ɓ����O�͂�F�݂̂ŁA���̌��ʂ͓��R�ł����A�A�����A���n�ɂ����Ă��A�����͂̎d�����l���邱�Ƃɂ��A��n�ɂ�����͊w�I�G�l���M�[�ۑ����Ɩ������Ȃ����ʂ������邱�Ƃ������Ă��܂��B
�����������Ƃ����d���Ɉ�v���܂��B�d�͂̎d���́A�d�͂̈ʒu�G�l���M�[�Ƃ��čl���Ă���̂ŁA�n�ɓ����O�͂�F�݂̂ŁA���̌��ʂ͓��R�ł����A�A�����A���n�ɂ����Ă��A�����͂̎d�����l���邱�Ƃɂ��A��n�ɂ�����͊w�I�G�l���M�[�ۑ����Ɩ������Ȃ����ʂ������邱�Ƃ������Ă��܂��B
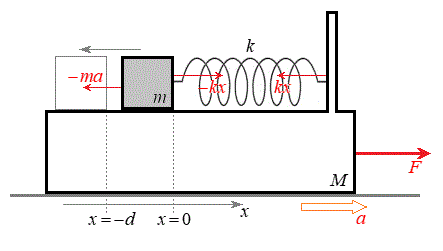 [2]�@��2�̗�́A�����͈͂�肾�����Ή����x(���n���猩�������x)�����ɂȂ�Ȃ���ł��B
[2]�@��2�̗�́A�����͈͂�肾�����Ή����x(���n���猩�������x)�����ɂȂ�Ȃ���ł��B����M�̉����ɌŒ肳�ꂽ�Y������A�Y�ɂ˒萔k�̂˂����t�����ċt�̒[�Ɏ���m�̕��̂����t�����Ă���B�S�ĐÎ~���Ă���Ƃ���ɊO��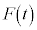 ��^���āA����������xa�ʼn^��������B�^�����n�܂��Ă���˂��ő�̐L�тɂȂ����Ƃ��̂˂̐L��d�����߂�B
��^���āA����������xa�ʼn^��������B�^�����n�܂��Ă���˂��ő�̐L�тɂȂ����Ƃ��̂˂̐L��d�����߂�B
���Ō���ƁA�˂̐L�т�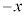 (�t�b�N�̖@�����Q��)�C���̂̉����x��b�Ƃ��āA���̂͊����͂���̂ŁA���̂̉^���������́A
(�t�b�N�̖@�����Q��)�C���̂̉����x��b�Ƃ��āA���̂͊����͂���̂ŁA���̂̉^���������́A �� 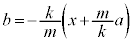 ����͊p�U����
����͊p�U����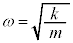 �C�U�����S
�C�U�����S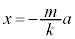 ���P�U����\���܂��B�˂̐L�т��ő�ɂȂ�܂ł̎���
���P�U����\���܂��B�˂̐L�т��ő�ɂȂ�܂ł̎���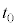 �͎�����
�͎�����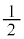 �ŁA
�ŁA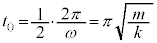 �C�͂���(
�C�͂���(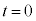 �C
�C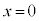 )�U���[�ɂ����̂ŁA�U��A�́A
)�U���[�ɂ����̂ŁA�U��A�́A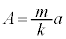
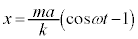 �@����@
�@����@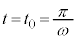 �̂Ƃ��A
�̂Ƃ��A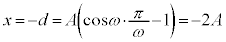
�� 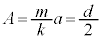 �@��
�@�� 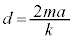 ......[��]���Ō���ƁA�^�����n�܂������_�ł�����
......[��]���Ō���ƁA�^�����n�܂������_�ł�����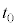 �ɂ����Ă��A���̂̉^���G�l���M�[��0�ł��B����
�ɂ����Ă��A���̂̉^���G�l���M�[��0�ł��B����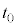 �ɂ�����˂̒e���G�l���M�[��
�ɂ�����˂̒e���G�l���M�[��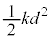 �ŁA�����͂������d����
�ŁA�����͂������d����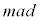 �C����đ��Ō����͊w�I�G�l���M�[�ۑ��́A
�C����đ��Ō����͊w�I�G�l���M�[�ۑ��́A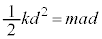 �@��
�@�� 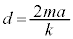
�ƂȂ�A�������ʂ������܂��B
������O�����猩�ĉ����Ƃǂ��Ȃ�ł��傤���H
�����̈ʒu(�˂̏k��)��x (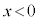 )�Ƃ��āA
)�Ƃ��āA
��̉^���������F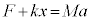 (a�F���)�@����A
(a�F���)�@����A
���̂̉^���������F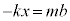 �@����B
�@����B �O�����猩�āA����t�ɂ������̑��x��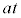 �C��̈ʒu(
�C��̈ʒu(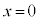 �̈ʒu)��
�̈ʒu)��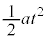 �C���̂̈ʒu�́A
�C���̂̈ʒu�́A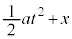
���Ō������x(���Α��x)�́A�@���A ������A���̂̑��x�́A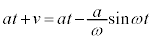 �C���̂̉����x�́A
�C���̂̉����x�́A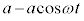
���Ō������̂̉����x(���Ή����x)�́A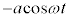
�˂̐L�т��ő�ɂȂ�܂ł̎��Ԃ�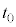 �Ƃ��āA���̂Ƃ��A�����猩�āA������̂����x��
�Ƃ��āA���̂Ƃ��A�����猩�āA������̂����x��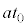 �A���̂̈ړ�������
�A���̂̈ړ�������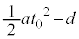 �@(
�@(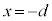 )�����猩�����̂̉����x
)�����猩�����̂̉����x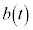 �C���x
�C���x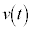 �́A
�́A 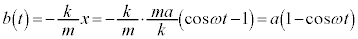 �@(�� �@�C�B)
�@(�� �@�C�B)�����猩�āA�͂��߂̃G�l���M�[��0�ŁA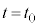 �ɂ͉^���G�l���M�[
�ɂ͉^���G�l���M�[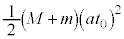 �ƒe���G�l���M�[
�ƒe���G�l���M�[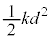 ������A
������A
��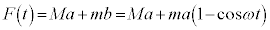 �����x
�����x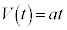 �œ����Ƃ��̎d���́A
�œ����Ƃ��̎d���́A ����āA��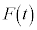 �̂����d�����A�^���G�l���M�[�ƒe���G�l���M�[�̘a�ɂȂ�A
�̂����d�����A�^���G�l���M�[�ƒe���G�l���M�[�̘a�ɂȂ�A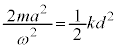 �C
�C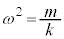 ���
���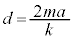 �������܂��B�ł����A
�������܂��B�ł����A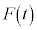 �C
�C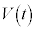 �����ԕω�����ꍇ�ɂ́A����Ō���Ǝd�����ϕ��v�Z�ɂȂ�A���Ō��ė͊w�I�G�l���M�[�ۑ����l��������v�Z�����N�Ȃ��Ƃɒ��ӂ��Ă��������B
�����ԕω�����ꍇ�ɂ́A����Ō���Ǝd�����ϕ��v�Z�ɂȂ�A���Ō��ė͊w�I�G�l���M�[�ۑ����l��������v�Z�����N�Ȃ��Ƃɒ��ӂ��Ă��������B
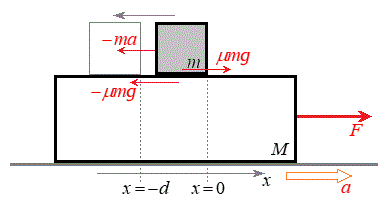 [3]�@�����͂����Ή����x����肾���A�G�l���M�[���ۑ����Ȃ��ꍇ�ł��B
[3]�@�����͂����Ή����x����肾���A�G�l���M�[���ۑ����Ȃ��ꍇ�ł��B���ɒu���ꂽ����M�̑��Ɏ���m�̕��̂��u����Ă���B���̂Ƒ�̊Ԃɂ́A���C�͂������B�ŏ��ɐÎ~���Ă��āA���x���������̊O��F���y�ڂ��Ĉ������xa��^����Ƃ��A�O�͂������n�߂Ă��玞��t �̊Ԃɕ��̂����œ����ψ�d�����߂�B�Î~���C�W��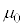 �C�����C�W��μ�ɂ��āA
�C�����C�W��μ�ɂ��āA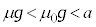 �Ƃ���ƁA���Ō���
�Ƃ���ƁA���Ō���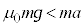 �ƂȂ�A�����͂��ő�Î~���C�͂��z���A���̂͑�������A���̂ɂ͓����C��
�ƂȂ�A�����͂��ő�Î~���C�͂��z���A���̂͑�������A���̂ɂ͓����C��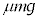 ������(���C�����Q��)
������(���C�����Q��)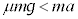 �����Ō��ĕ��͍̂��ɓ����B
�����Ō��ĕ��͍̂��ɓ����B
��ƕ��̂̍��W�̌��_����v�����A���̂̉����x��b�Ƃ��āA
���Ō�����̉^���������́A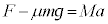 �@����@
�@����@
���Ō������̂̉^���������́A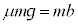 �@��
�@�� 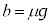 �@����A
�@����A
�����猩�āA��̈ʒu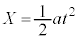 �C��̑��x
�C��̑��x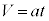 �C���̂̈ʒu
�C���̂̈ʒu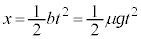 �C���̂̑��x
�C���̂̑��x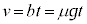
���Ō������̂̉����x��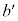 �Ƃ��āA�^���������F
�Ƃ��āA�^���������F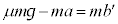
�� 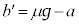 ���Ō������̂̑��Έʒu
���Ō������̂̑��Έʒu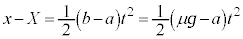 �C���Α��x
�C���Α��x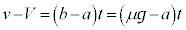 �@����B
�@����B 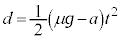 ......[��]�@����C
......[��]�@����C���Ō��ăG�l���M�[���l���Ă݂܂��B�B���A����t �ɂ����镨�̂̉^���G�l���M�[��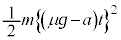 �C�����͂̂����d����
�C�����͂̂����d����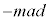 �C�����C��(���̂̉^�������Ɏd��������)�̂����d����
�C�����C��(���̂̉^�������Ɏd��������)�̂����d����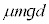 �C���Ō����G�l���M�[�̌����̎��́A
�C���Ō����G�l���M�[�̌����̎��́A �C�Ɠ������ʂ������܂��B
�����猩�ăG�l���M�[���l����ƁA����t �o�ߌ�̉^���G�l���M�[�́A�A���A
�@���A��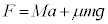 �̂����d���F
�̂����d���F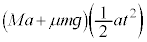 x���������̖��C��
x���������̖��C��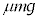 �����̂ɂ����d��
�����̂ɂ����d��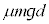
�����猩���G�l���M�[�̌����̎��́A �� 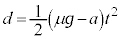 �C�Ɠ������ʂɂȂ�܂����A���ōl����ꍇ�����ʓ|�ł��B
�C�Ɠ������ʂɂȂ�܂����A���ōl����ꍇ�����ʓ|�ł��B
[4]�@���́A�����͂����łȂ��A���Ή����x�����łȂ���ł��B
������'22�N[3]�@����Ɏ���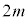 �̑䂪����A���Ƒ�̊Ԃɖ��C�͓����Ȃ��B����m�̏����Ƒ��̕ǂ��˒萔k�̂˂łȂ��A�ǂɌ����ď����ɑ��x
�̑䂪����A���Ƒ�̊Ԃɖ��C�͓����Ȃ��B����m�̏����Ƒ��̕ǂ��˒萔k�̂˂łȂ��A�ǂɌ����ď����ɑ��x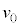 ��^����B�ŏ��ɂ˂��ł��k���̂˂̏k��d�����߂�B
��^����B�ŏ��ɂ˂��ł��k���̂˂̏k��d�����߂�B
�˂��ł��k�Ƃ��̏����Ƒ�̑��x��v (�����͑�ɑ��Ď~�܂�̂ŗ��҂̑��x�͈�v����)�Ƃ��܂��B�ŏ��ɂ˂��ł��k�Ƃ��ƁA�ŏ��̏�ԂƂ̉^���ʕۑ����A 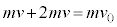 �@��
�@�� 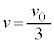 �@����@
�@����@�ŏ��ɂ˂��ł��k�Ƃ��ƁA�ŏ��̏�ԂƂ̗͊w�I�G�l���M�[�ۑ����A
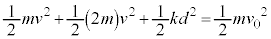 �@����A
�@����A�@��p���āA
�� 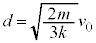 ......[��]�@����B
......[��]�@����B
�^���������𗧂Ăčl���Ă݂܂��B��̉����x��A�C�˂̏k�݂�x�Ƃ��A����Ō��āA��̉^���������́A 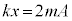 �@����C
�@����C���Ō��������̉����x��a�Ƃ��A���Ō��āA�����̉^���������́A
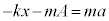 �@����D
�@����D�C�{�D���A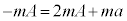 �@��
�@�� 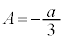 �D�ɑ�����āA
�D�ɑ�����āA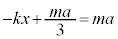 �@��
�@�� 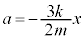 ����́A�p�U����
����́A�p�U����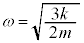 �̒P�U����\���܂��B
�̒P�U����\���܂��B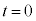 �ɂ�����
�ɂ�����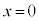 ��
��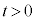 ��
��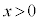 �ɂȂ�Ƃ��āA
�ɂȂ�Ƃ��āA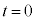 �̈ʒu�������̐U�����S(�����ő�)�ŁA�ŏ��ɂ˂��ł��k�Ƃ��A�U���[�ł��B�P�U���̐U����d�ł��B�P�U���̌����F
�̈ʒu�������̐U�����S(�����ő�)�ŁA�ŏ��ɂ˂��ł��k�Ƃ��A�U���[�ł��B�P�U���̐U����d�ł��B�P�U���̌����F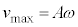 ���A
���A 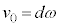 �@��
�@�� 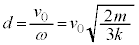
�B�������܂��B
�����ŁA�A�̑���ɁA���Ō����G�l���M�[�ۑ����l���Ă݂܂��B
���ł́A�ŏ��͏����̉^���G�l���M�[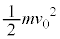 �C�ŏ��ɂ˂��ł��k�Ƃ��ɂ́A�����͑�ɑ��ĐÎ~����̂ŁA�^���G�l���M�[�͂���܂���B�˂̒e���G�l���M�[�́A�˂�d�k��ł���̂�
�C�ŏ��ɂ˂��ł��k�Ƃ��ɂ́A�����͑�ɑ��ĐÎ~����̂ŁA�^���G�l���M�[�͂���܂���B�˂̒e���G�l���M�[�́A�˂�d�k��ł���̂�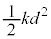 �ł��B�e���G�l���M�[���l����̂ŁA�˂̒e���͂������ƁA��������͍͂������̊�����
�ł��B�e���G�l���M�[���l����̂ŁA�˂̒e���͂������ƁA��������͍͂������̊�����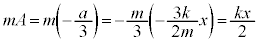 �݂̂ł��B�����͂̂����d��W�́A�ŏ��ɂ˂��ł��k�ގ�����
�݂̂ł��B�����͂̂����d��W�́A�ŏ��ɂ˂��ł��k�ގ�����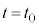 �Ƃ��āA
�Ƃ��āA 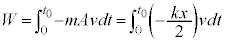 �@(�����͍͂������Ȃ̂Ń}�C�i�X����)
�@(�����͍͂������Ȃ̂Ń}�C�i�X����)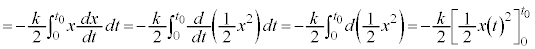
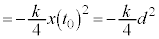 (f-x�O���t�ŎO�p�`�̖ʐςƂ��ċ��߂Ă�OK)
(f-x�O���t�ŎO�p�`�̖ʐςƂ��ċ��߂Ă�OK)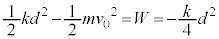 �@��
�@�� 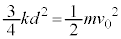
�ƂȂ�A���Ō��Ċ����͂̎d�����l���Ă��B�������܂��B���̗�ł́A�����͂����Ԉˑ��E�ʒu�ˑ�����̂ŁA��n�ōl��������v�Z�����N�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B