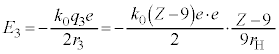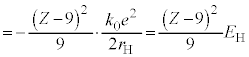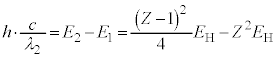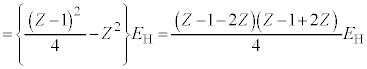��啨��'22�N�O��[3]
�ȉ���A��B�̗����̖��ɉ���B�Ȃ�A��B�͓Ɨ��������e�̖��ł���B
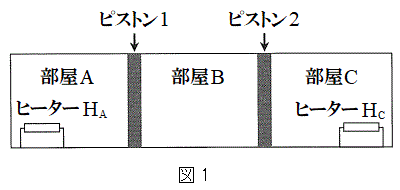 A�D�@�}1�̂悤�ȌŒ肳�ꂽ�V�����_�[���ɁA�Ȃ߂炩�ɓ���2�̃s�X�g��������B�s�X�g���Ŏd��ꂽ�V�����_�[���̊e�̈���A�����畔��A�C����B�C����C�Ƃ�ԁB����A�ƕ���B���s�X�g��1�C����B�ƕ���C���s�X�g��2���d��B����A�ƕ���C�̒��ɂ���q�[�^�[
A�D�@�}1�̂悤�ȌŒ肳�ꂽ�V�����_�[���ɁA�Ȃ߂炩�ɓ���2�̃s�X�g��������B�s�X�g���Ŏd��ꂽ�V�����_�[���̊e�̈���A�����畔��A�C����B�C����C�Ƃ�ԁB����A�ƕ���B���s�X�g��1�C����B�ƕ���C���s�X�g��2���d��B����A�ƕ���C�̒��ɂ���q�[�^�[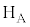 �ƃq�[�^�[
�ƃq�[�^�[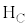 ��p���āA���ꂼ��̕����̓����ɂ���C�̂����M���邱�Ƃ��ł���B�V�����_�[�A�s�X�g���A�q�[�^�[�����킹�đ��u�Ƃ�Ԃ��Ƃɂ���B���u�̔M�e�ʂ͖����ł���B
��p���āA���ꂼ��̕����̓����ɂ���C�̂����M���邱�Ƃ��ł���B�V�����_�[�A�s�X�g���A�q�[�^�[�����킹�đ��u�Ƃ�Ԃ��Ƃɂ���B���u�̔M�e�ʂ͖����ł���B���̑��u�̃s�X�g�����A�O�����瓮��������Œ肵���肷�邱�Ƃ��ł���B�s�X�g�����q�[�^�[�ɂԂ���Ȃ��͈͂œ����ꍇ�ɂ��čl����B�e�����ɂ͂��ꂼ��1�������A����̗��z�C�̂������Ă���B���̗��z�C�̂̒�σ�����M��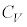 �C�舳������M��
�C�舳������M��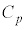 �Ƃ���A�C�̒萔��R�Ƃ���B
�Ƃ���A�C�̒萔��R�Ƃ���B �T�D���̑��u���Ή��x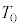 �̊��ɒu���āA���ԂɈȉ��̑��������B�͂��߁A����A�CB�CC�̋C�̂̑̐ς͂������
�̊��ɒu���āA���ԂɈȉ��̑��������B�͂��߁A����A�CB�CC�̋C�̂̑̐ς͂������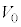 �ł������B���u�͊O���ɔM��ʂ����̂Ƃ���B�ȉ��̖�ɓ�����B
�ł������B���u�͊O���ɔM��ʂ����̂Ƃ���B�ȉ��̖�ɓ�����B
 �}2�ɁA��Ή��xT�����ł���1�����̗��z�C�̂̈��͂Ƒ̐ς̊W�������B�ɂ������ẮA�}2�̎ΐ����̖ʐς�
�}2�ɁA��Ή��xT�����ł���1�����̗��z�C�̂̈��͂Ƒ̐ς̊W�������B�ɂ������ẮA�}2�̎ΐ����̖ʐς�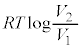 �ł��邱�Ƃ�p���Ă悢�B�����ł�
�ł��邱�Ƃ�p���Ă悢�B�����ł�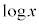 �́A
�́A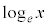 �ł���Be (
�ł���Be (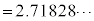 )�͖������ł���Ae���Ƃ���ΐ������R�ΐ��Ƃ����B
)�͖������ł���Ae���Ƃ���ΐ������R�ΐ��Ƃ����B
��1�@�܂��A�s�X�g��2���Œ肵����ԂŃs�X�g��1���\���ɂ������ƉE�ɓ������A����A�̋C�̂̑̐ς�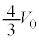 �ƂȂ����Ƃ���Ńs�X�g��1���Œ肵���B���̂Ƃ��́A����B�̋C�̂̈���
�ƂȂ����Ƃ���Ńs�X�g��1���Œ肵���B���̂Ƃ��́A����B�̋C�̂̈���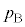 ���AR�C
���AR�C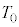 �C
�C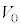 ��p���ĕ\���B
��p���ĕ\���B ��2�@��1�̑���ɂ���ăs�X�g��1������B�̋C�̂ɂ����d��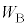 ���AR�C
���AR�C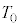 �C
�C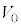 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B ��3�@��1�ōŌ�Ƀs�X�g��1���Œ肵����Ԃ���s�X�g��2���\���ɂ������ƍ��ɓ������A����C�̋C�̂̑̐ς�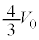 �ƂȂ����Ƃ���Ńs�X�g��2���Œ肵���B��1�̑�����n�߂�O���炱���ɂ�����܂ł̕ω��ɂ��āA�ȉ��̗ʂ����߂�B�K�v�ł���AR�C
�ƂȂ����Ƃ���Ńs�X�g��2���Œ肵���B��1�̑�����n�߂�O���炱���ɂ�����܂ł̕ω��ɂ��āA�ȉ��̗ʂ����߂�B�K�v�ł���AR�C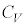 �C
�C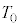 �C
�C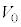 ��p���Ă悢�B
��p���Ă悢�B (a) 3�̕������ɂ���C�̂̓����G�l���M�[�̑����ʂ̑��a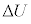
(b) ���u����O���ɕ��o���ꂽ�M�̑���Q
�U�D�ӂ����сA�e�����̋C�̂̑̐ς�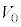 �C��Ή��x��
�C��Ή��x��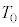 �ł����Ԃ��瑀����n�߂�B����ȍ~�͑��u��f�M�ނŕ����A�V�����_�[�̊O�ǂ�ʂ����O���Ƃ̔M�̂��Ƃ肪�N���Ȃ����̂Ƃ���B2�̃s�X�g���͌Œ肳��Ă��Ȃ��B�s�X�g���͔M��ʂ��Ȃ��f�ނłł��Ă���A�����̊Ԃł̔M�̂��Ƃ�͂Ȃ����̂Ƃ���B���̂Ƃ��̑��u�ƋC�̂̏�Ԃ����(��)�Ƃ���B
�ł����Ԃ��瑀����n�߂�B����ȍ~�͑��u��f�M�ނŕ����A�V�����_�[�̊O�ǂ�ʂ����O���Ƃ̔M�̂��Ƃ肪�N���Ȃ����̂Ƃ���B2�̃s�X�g���͌Œ肳��Ă��Ȃ��B�s�X�g���͔M��ʂ��Ȃ��f�ނłł��Ă���A�����̊Ԃł̔M�̂��Ƃ�͂Ȃ����̂Ƃ���B���̂Ƃ��̑��u�ƋC�̂̏�Ԃ����(��)�Ƃ���B �܂��A�q�[�^�[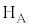 ��p���ĕ���A�̋C�̂��������Ɖ��M�����Ƃ���A2�̃s�X�g�����������Ɠ����n�߂��B���M����߂Ă���\���Ɏ��Ԃ��o���A2�̃s�X�g�����Î~�����Ƃ��̑��u�ƋC�̂̏�Ԃ��A���(��)�Ƃ���B����ɁA�q�[�^�[
��p���ĕ���A�̋C�̂��������Ɖ��M�����Ƃ���A2�̃s�X�g�����������Ɠ����n�߂��B���M����߂Ă���\���Ɏ��Ԃ��o���A2�̃s�X�g�����Î~�����Ƃ��̑��u�ƋC�̂̏�Ԃ��A���(��)�Ƃ���B����ɁA�q�[�^�[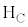 ��p���ĕ���C�̋C�̂��������Ɖ��M�����Ƃ���A2�̃s�X�g�����������Ɠ����n�߂��B���M����߂Ă���\���Ɏ��Ԃ��o���A2�̃s�X�g�����Î~�����Ƃ��̑��u�ƋC�̂̏�Ԃ��A���(��)�Ƃ���B���(��)�ɂ����āA����A�CB�CC�̋C�̂̑̐ϔ��4�F1�F4�ɂȂ��Ă����B�ȉ��̖�ɓ�����B
��p���ĕ���C�̋C�̂��������Ɖ��M�����Ƃ���A2�̃s�X�g�����������Ɠ����n�߂��B���M����߂Ă���\���Ɏ��Ԃ��o���A2�̃s�X�g�����Î~�����Ƃ��̑��u�ƋC�̂̏�Ԃ��A���(��)�Ƃ���B���(��)�ɂ����āA����A�CB�CC�̋C�̂̑̐ϔ��4�F1�F4�ɂȂ��Ă����B�ȉ��̖�ɓ�����B
�ɂ������ẮAp�𗝑z�C�̂̈��́AV�𗝑z�C�̂̑̐ςƂ���ƁA�f�M�ߒ��ɂ�����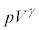 �����ɕۂ���邱�Ƃ�p���Ă悢�B�������A
�����ɕۂ���邱�Ƃ�p���Ă悢�B�������A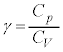 �ł���B
�ł���B
��4�@���(��)�ɂ����镔��B�̋C�̂̐�Ή��x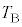 ���Aγ�C
���Aγ�C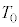 �̂����K�v�Ȃ��̂�p���ĕ\���B
�̂����K�v�Ȃ��̂�p���ĕ\���B ��5�@�q�[�^�[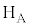 ������A�̋C�̂ɗ^�����M��
������A�̋C�̂ɗ^�����M��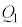 �C�q�[�^�[
�C�q�[�^�[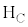 ������C�̋C�̂ɗ^�����M��
������C�̋C�̂ɗ^�����M��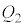 �Ƃ���B
�Ƃ���B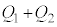 ��γ�C
��γ�C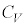 �C
�C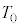 ��p���ĕ\���B
��p���ĕ\���B ��6�@���(��)�ɂ����镔��A�CB�CC�̋C�̂̑̐ς��A���ꂼ��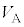 �C
�C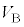 �C
�C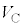 �Ƃ���B
�Ƃ���B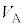 �F
�F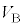 �F
�F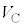 ���A�ł��ȒP�Ȑ����̔�ŕ\���B
���A�ł��ȒP�Ȑ����̔�ŕ\���B
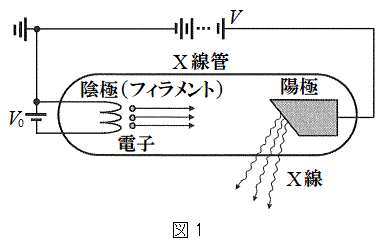 B�DX���͉����⎇�O�������g���̒Z�����ł���A���������d�q���̕\�ʂɏƎ˂���Ɣ�������B
B�DX���͉����⎇�O�������g���̒Z�����ł���A���������d�q���̕\�ʂɏƎ˂���Ɣ�������B�T�D�}1�̂悤�ȑ��u���g�p���āAX����������ꍇ�ɂ��čl����B�������A�t�B�������g�̓d���̓d��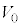 �́A�����d���̓d��V�ɑ��ď\���ɏ������B
�́A�����d���̓d��V�ɑ��ď\���ɏ������B 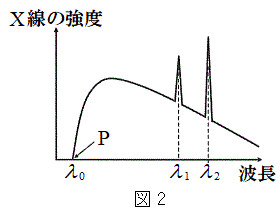 �A�ɁE�z�ɊԂɍ��d��V���������X�����������A��������X���̔g���Ƃ��̋��x�̊W(X���g���X�y�N�g��)�́A�}2�̂悤�ɂȂ�B�A��X���ƁA����̔g���ɋ������x�����ŗLX��(����X��)���������邱�Ƃ��킩��B�d�q�̎��ʂ�m�C�d�q�̓d�ׂ�
�A�ɁE�z�ɊԂɍ��d��V���������X�����������A��������X���̔g���Ƃ��̋��x�̊W(X���g���X�y�N�g��)�́A�}2�̂悤�ɂȂ�B�A��X���ƁA����̔g���ɋ������x�����ŗLX��(����X��)���������邱�Ƃ��킩��B�d�q�̎��ʂ�m�C�d�q�̓d�ׂ�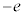 �C�v�����N�萔��h�C���̑�����c�Ƃ��āA�ȉ��̖�ɓ�����B
�C�v�����N�萔��h�C���̑�����c�Ƃ��āA�ȉ��̖�ɓ�����B
��7�@�}2�Ɏ�����Ă���_P�̔g��(�ŒZ�g��)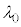 ��h�Cc�Cm�Ce�����V�̂����K�v�Ȃ��̂�p���ĕ\���B
��h�Cc�Cm�Ce�����V�̂����K�v�Ȃ��̂�p���ĕ\���B 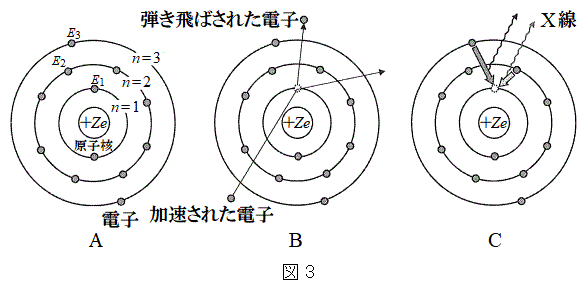 �U�D�}3�̂悤�Ȍ��q���f�����g���āA���q�ԍ���Z (
�U�D�}3�̂悤�Ȍ��q���f�����g���āA���q�ԍ���Z (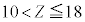 )�̌��q�����o����ŗLX�����l����B���S�ɓd��
)�̌��q�����o����ŗLX�����l����B���S�ɓd��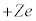 �������q�j������A���̂܂���d�q�������~�^�����Ă���B
�������q�j������A���̂܂���d�q�������~�^�����Ă���B
�O����̓d�q�́A���̗ʎq�����ɂ��������B
�ʎq�������q���̓d�q�́A�~�O���̎��̒����������g�̔g����n�{(n�͐��̐���)�ł���Ƃ��ɁA����ԂƂ��Ĉ���ɑ��݂ł���B
�~�O����̓d�q�́A�}3A�̂悤�ɁA��܂�����(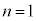 �̋O���ɂ�2�A
�̋O���ɂ�2�A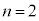 �̋O���ɂ�8�A���)�����A�Ⴂ�G�l���M�[���ʂ����Ԃ��߂Ă����B����(n�Ԗ�)�̋O���ɂ���d�q�́A�����G�l���M�[����
�̋O���ɂ�8�A���)�����A�Ⴂ�G�l���M�[���ʂ����Ԃ��߂Ă����B����(n�Ԗ�)�̋O���ɂ���d�q�́A�����G�l���M�[����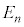 �����Ƃ���(
�����Ƃ���(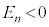 )�B�~�O���ɂ���d�q�ɂ́A���q�j�Ƃ̊ԂɃN�[�����͂��͂��炫�A���̓d�q����͎͂Ȃ��Ƃ���B�������A
)�B�~�O���ɂ���d�q�ɂ́A���q�j�Ƃ̊ԂɃN�[�����͂��͂��炫�A���̓d�q����͎͂Ȃ��Ƃ���B�������A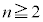 �̋O���ɂ���d�q����́A�������̋O���ɂ���d�q�̐��̕������A���q�j�̓d�ׂ�ł������悤�Ɍ����邽�߁A�N�[�����͕͂����(�Ⴆ�A�}3A��
�̋O���ɂ���d�q����́A�������̋O���ɂ���d�q�̐��̕������A���q�j�̓d�ׂ�ł������悤�Ɍ����邽�߁A�N�[�����͕͂����(�Ⴆ�A�}3A��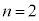 �̋O���ɂ���d�q����́A���q�j�̓d�ׂ�
�̋O���ɂ���d�q����́A���q�j�̓d�ׂ�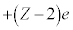 �Ɍ�����)�B
�Ɍ�����)�B
�ŗLX���́A���̐U���������ɂ��������ĕ��o�����B �U���������}3B�̂悤�ɁA�������ꂽ�d�q�����q���̓d�q��e��������Ƃ��A�}3C�̂悤�ɁA�O���̋O���̓d�q���������̋O���Ɉڂ��āA�G�l���M�[���ʍ��ɑΉ�����U������X�������o�����B
�O����̓d�q�̑����́A���̑���c���\���ɒx���Ƃ��āA�ȉ��̖�ɓ�����B
��8�@�}3A��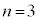 �̋O���̔��a��
�̋O���̔��a��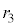 �Ƃ����Ƃ��A�N�[�����͂Ɖ��S�͂̂荇���̊W����A
�Ƃ����Ƃ��A�N�[�����͂Ɖ��S�͂̂荇���̊W����A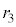 ���Ah�Cm�Ce�CZ�C�^�̃N�[�����̖@���̔��萔
���Ah�Cm�Ce�CZ�C�^�̃N�[�����̖@���̔��萔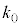 ��p���ĕ\���B
��p���ĕ\���B ��9�@�}3A�̃G�l���M�[����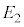 �C
�C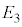 ���A���f���q(
���A���f���q(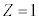 )�̊���Ԃ̓d�q�̃G�l���M�[����
)�̊���Ԃ̓d�q�̃G�l���M�[����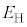 ��Z�݂̂��g���Ă��ꂼ��\���B�������A�N�[�����͂ɂ��ʒu�G�l���M�[�͖��������[��(�)�Ƃ���B
��Z�݂̂��g���Ă��ꂼ��\���B�������A�N�[�����͂ɂ��ʒu�G�l���M�[�͖��������[��(�)�Ƃ���B ��10�@�}2�Ɏ�����Ă���ŗLX����2�̃s�[�N�́A�}3C�̂悤�ɁA�d�q��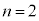 ����
����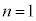 �ƁA
�ƁA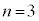 ����
����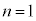 �̋O���ֈڂ�Ƃ��ɕ��o�����X���ɑΉ�����B�ŗLX�������o����钼�O�ɂ́A
�̋O���ֈڂ�Ƃ��ɕ��o�����X���ɑΉ�����B�ŗLX�������o����钼�O�ɂ́A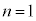 �̋O���ɂ���d�q�̐���1�ł��邱�Ƃɒ��ӂ��ČŗLX���̔g��
�̋O���ɂ���d�q�̐���1�ł��邱�Ƃɒ��ӂ��ČŗLX���̔g��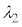 ���A
���A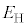 �CZ�Ch�Cc���g���ĕ\���B
�CZ�Ch�Cc���g���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@A�DB�D�ǂ���̖������Ԃ������Ă������l����̂ł�������[�����Ȃ̂ł����A���G�����āA��蕶�ɐe�ȃq���g������Ƃ͌����Ă��A�������Ƃ��Ă͖����ł��B�������ł́A���Ԃ�����������g��Ő[���肵�Ȃ����������ł��B
A�D�T�D����A�CB�CC�̈��͂�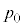 �Ƃ��āA�͂��߂̏�Ԃ���ԕ������́A
�Ƃ��āA�͂��߂̏�Ԃ���ԕ������́A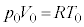 �@����@
�@����@ ���@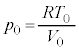 �@����A
�@����A ��Ή��x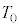 �͕ς��Ȃ��̂ŁA��1�C��2�C��3�������ω��ł��B
�͕ς��Ȃ��̂ŁA��1�C��2�C��3�������ω��ł��B
��1�@�����̕���B�̈��͂�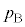 �Ƃ���ƁA����B�̑̐ς�
�Ƃ���ƁA����B�̑̐ς�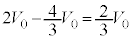 �Ȃ̂ŁA��ԕ������́A
�Ȃ̂ŁA��ԕ������́A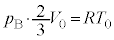 �@����B
�@����B �B���@���A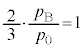 �C�A��p���āA
�C�A��p���āA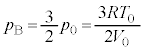 ......[��]
......[��]
��2�@���x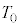 �ŁA����B�̑̐ς�
�ŁA����B�̑̐ς�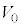 ����
����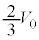 �܂ŕω�����̂Ő}2�̎ΐ����̖ʐς̃q���g����A�s�X�g��1������B�̋C�̂ɂ����d���A�����A����B���C�̂����ꂽ�d��
�܂ŕω�����̂Ő}2�̎ΐ����̖ʐς̃q���g����A�s�X�g��1������B�̋C�̂ɂ����d���A�����A����B���C�̂����ꂽ�d��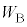 �́A
�́A 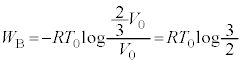 ......[��]�@����C
......[��]�@����C
��3�@�s�X�g��2�����Ă���ԂɁA���x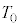 �ŕ���C�̑̐ς�
�ŕ���C�̑̐ς�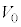 ����
����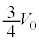 �܂ŕς��̂ŁA����C�̋C�̂������d���́A
�܂ŕς��̂ŁA����C�̋C�̂������d���́A 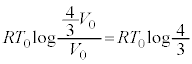 �@����E
�@����E���̊Ԃɕ���B�̑̐ς�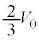 ����
����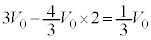 �܂ŕς��̂ŁA����B�̋C�̂������d���́A
�܂ŕς��̂ŁA����B�̋C�̂������d���́A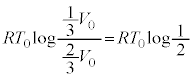 �@����F
�@����F
�C�C�D�C�E�C�F���A��1�̑�����n�߂�O���炱���ɂ�����܂ł̕ω��ɂ��āA���u���̋C�̂̂����d���̑��aW�́A 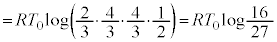 �@����G
�@����G(a) ��1�̑�����n�߂�O���炱���ɂ�����܂ŁA���x���Ȃ̂ŁA�����G�l���M�[�̕ω��͂���܂���B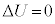 ......[��]
......[��] (b) ���u����O���ɕ��o���ꂽ�M�ʂ�Q�Ȃ̂ŁA���u���̋C�̂��z�������M��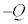 �ł��B�M�͊w��1�@�����A
�ł��B�M�͊w��1�@�����A �C�G��(a)�̌��ʂ��A
�C�G��(a)�̌��ʂ��A 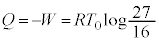 ......[��]
......[��]
�U�D(���ӁF�����������߁A���̔ԍ����T�D�ƇU�D�œƗ��ɂ��܂�)���(��)�ł́A�e�����̑̐ς�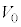 �C���x��
�C���x��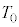 �ŁA2�̃s�X�g���͌Œ肳��Ă��Ȃ��̂ŁA�s�X�g���ɓ����͂̂肠�����A�e�����̈��͓͂������A�����
�ŁA2�̃s�X�g���͌Œ肳��Ă��Ȃ��̂ŁA�s�X�g���ɓ����͂̂肠�����A�e�����̈��͓͂������A�����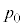 �Ƃ��܂��B�e�����̏�ԕ������́A
�Ƃ��܂��B�e�����̏�ԕ������́A 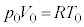 �@����@
�@����@���(��)�ł͏��(��)�Ɠ������A�s�X�g���ɓ����͂̂肠�����A�e�����̈��͓͂������A�����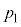 �Ƃ��܂��B����A�̑̐ς�
�Ƃ��܂��B����A�̑̐ς�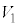 �Ƃ��A�܂��A����B�C����C�͓���̏�ԂŁA�����̑̐ς�
�Ƃ��A�܂��A����B�C����C�͓���̏�ԂŁA�����̑̐ς�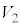 �C���x��
�C���x��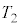 �Ƃ��܂��B
�Ƃ��܂��B
���(��)�ɂ����镔��A�̏�ԕ������F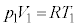 �@����A
�@����A
���(��)�ɂ����镔��B�C����C�̏�ԕ������F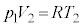 �@����B�f�M�ߒ��ł�
�@����B�f�M�ߒ��ł�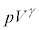 �����(�|�A�b�\���̊W��)�ɕۂ����Ƃ����q���g�ɂ��A(��)����(��)�܂ŁA����B�C����C�͒f�M�ω�������̂ŁA
�����(�|�A�b�\���̊W��)�ɕۂ����Ƃ����q���g�ɂ��A(��)����(��)�܂ŁA����B�C����C�͒f�M�ω�������̂ŁA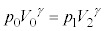 �@����C
�@����C
���(��)�ł́A����A�CB�CC�̑̐ϔ䂪4�F1�F4�Ȃ̂ŁA����A�CC�̑̐ς�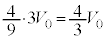 �C����B�̑̐ς�
�C����B�̑̐ς�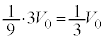 �ł��B���̏�Ԃł��A�s�X�g���ɓ����͂̂肠�����A�e�����̈��͓͂������A�����
�ł��B���̏�Ԃł��A�s�X�g���ɓ����͂̂肠�����A�e�����̈��͓͂������A�����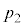 �Ƃ��܂��B����A�CB�CC�̉��x��
�Ƃ��܂��B����A�CB�CC�̉��x��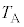 �C
�C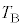 �C
�C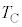 �Ƃ��܂��B
�Ƃ��܂��B
���(��)�ɂ����镔��A�̏�ԕ������F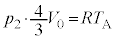 �@����D
�@����D
���(��)�ɂ����镔��B�̏�ԕ������F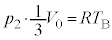 �@����E
�@����E
���(��)�ɂ����镔��C�̏�ԕ������F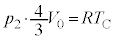 �@����F
�@����F
����A�͒f�M�ω�������̂ŁA�|�A�b�\���̊W�����A 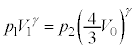 �@����G
�@����G����B�͒f�M�ω�������̂ŁA�|�A�b�\���̊W�����A
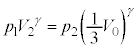 �@����H
�@����H�D�C�F���A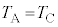 �@����I
�@����I
�E���D���A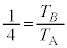 �@��
�@�� 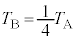 �@����J
�@����J
�C�C�H���A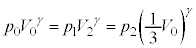 �@��
�@�� 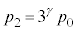 �@����K
�@����K
��4�@�K���E�ɑ�����āA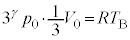 �@����L
�@����L �L���@���A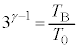 �@��
�@�� 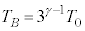 ......[��]
......[��]
��5�@�I�C�J���A
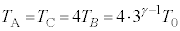
���(��)������(��)�܂ŁA����A�CC�̋C�̂̓����G�l���M�[�̕ω�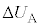 �C
�C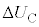 �́A
�́A ��4�̌��ʂ�p���āA����B�̋C�̂̓����G�l���M�[�̕ω�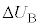 �́A
�́A ���(��)������(��)�܂ŁA���u���̋C�̂̓����G�l���M�[�̕ω��̑��a�́A
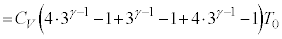
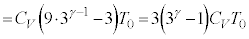 �@����M
�@����M���u�S�̂ł́A�C�̂̑��̐ςɕω��͂Ȃ��A���u���̋C�̂��O���ɂ����d����0
����āA�M�͊w��1�@�����A�q�[�^�[�����u���̋C�̂ɗ^�����M�A�������u���̋C�̂��z�������M�́A�M���A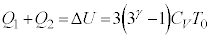 ......[��]
......[��]
��6�@�G���H���A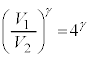 �@��
�@�� 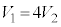
���(��)�ɂ����āA����B�C����C�̑̐ς͓�����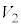 �ŁA
�ŁA 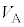 �F
�F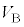 �F
�F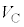 =
=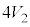 �F
�F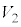 �F
�F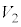 = 4�F1�F1 .......[��]
= 4�F1�F1 .......[��]
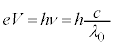 �@��
�@�� 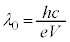 ......[��]
......[��]
�U�D��8�@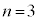 �݂̏̂�����Ă���̂ł����A
�݂̏̂�����Ă���̂ł����A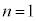 �̏ꍇ��
�̏ꍇ��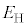 (
(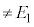 )�C
)�C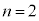 �̏ꍇ��
�̏ꍇ��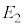 �C
�C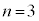 �̏ꍇ��
�̏ꍇ��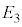 �����ׂ�K�v������̂ŁA�܂Ƃ߂čl���邱�Ƃɂ��܂��B
�����ׂ�K�v������̂ŁA�܂Ƃ߂čl���邱�Ƃɂ��܂��B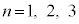 �̋O���̔��a��
�̋O���̔��a��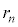 �C�d�q���O�������鑬����
�C�d�q���O�������鑬����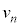 �Ƃ��܂��B
�Ƃ��܂��B 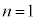 �̋O����̓d�q�ɂƂ��āA
�̋O����̓d�q�ɂƂ��āA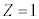 (���f)�̏ꍇ���܂߂āA���q�j�̓d�ׂ�
(���f)�̏ꍇ���܂߂āA���q�j�̓d�ׂ�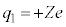 �ł��B
�ł��B
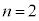 �̋O����̓d�q����A���q�j�̓d�ׂ�
�̋O����̓d�q����A���q�j�̓d�ׂ�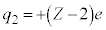 �ł���悤�Ɍ����܂��B
�ł���悤�Ɍ����܂��B
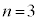 �̋O����̓d�q����A���q�j�̓d�ׂ�
�̋O����̓d�q����A���q�j�̓d�ׂ�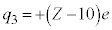 �ł���悤�Ɍ����܂��B
�ł���悤�Ɍ����܂��B
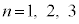 �̋O����̓d�q�����q�j�̓d�ׂ�����N�[�������́A
�̋O����̓d�q�����q�j�̓d�ׂ�����N�[�������́A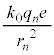 �ł��B�d�q�̑�����v�Ƃ��āA���S����
�ł��B�d�q�̑�����v�Ƃ��āA���S����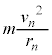 �ł��B�����̂肠�����A
�ł��B�����̂肠�����A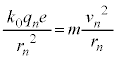 �@����@
�@����@
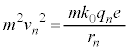 �@����A
�@����A
���������[���Ƃ��āA�d�q���ʒu�G�l���M�[�́A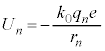
�d�q�̃G�l���M�[���ʂ́A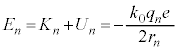 �@����C
�@����C
�B��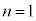 �Ƃ��āA
�Ƃ��āA 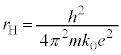 �@����D
�@����D�܂��A�C���A
�����ŁA���f���q(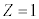 )�̊����(
)�̊����(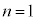 )�̓d�q�̃G�l���M�[����
)�̓d�q�̃G�l���M�[����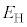 �́A
�́A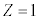 �C
�C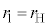 �Ƃ��āA
�Ƃ��āA 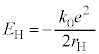 �@����E
�@����E�B��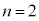 �Ƃ��A�D��p���āA
�Ƃ��A�D��p���āA ����ƇC�C�E���A
�� 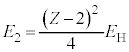 ......[��]
......[��] �B��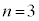 �Ƃ��A�D��p���āA
�Ƃ��A�D��p���āA ����ƇC�C�E���A
�� 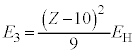 ......[��]
......[��]
��10�@��蕶�̃q���g�ł����A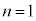 �̋O���ɂ���d�q�̐���1�ƍl����Ƃ������Ƃ́A
�̋O���ɂ���d�q�̐���1�ƍl����Ƃ������Ƃ́A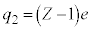 �C
�C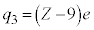 �C�J�ڌ�ɂ��Ă�
�C�J�ڌ�ɂ��Ă�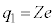 �Ƃ��čl����Ƃ������Ƃł��B
�Ƃ��čl����Ƃ������Ƃł��B ��8�C��9�̌������e�ŁA
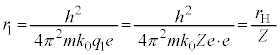 (�� �D)
(�� �D)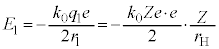
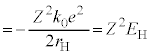 (�� �E)
(�� �E)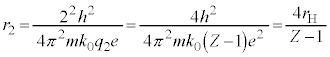 (�� �B�C�D)
(�� �B�C�D)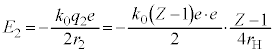
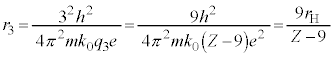 (�� �B)
(�� �B)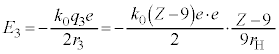
�ŗLX������������Ƃ��̃G�l���M�[�J�ڂ́A�}3C��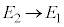 �C
�C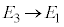 ���l���܂��B�ŗLX���̔g����λ�Ƃ��āA�ŗLX�����q�̃G�l���M�[�́A
���l���܂��B�ŗLX���̔g����λ�Ƃ��āA�ŗLX�����q�̃G�l���M�[�́A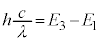 �C���邢�́A
�C���邢�́A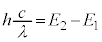 �ŗ^�����܂����A�}2�ɂ�����
�ŗ^�����܂����A�}2�ɂ�����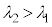 �Ȃ̂ŁA
�Ȃ̂ŁA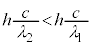 ���A�g����
���A�g����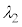 �ƂȂ�̂̓G�l���M�[���̏�������
�ƂȂ�̂̓G�l���M�[���̏�������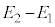 �ŁA
�ŁA �� 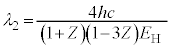 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 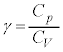 �ł���B
�ł���B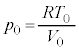 �@����A
�@����A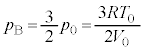 ......[��]
......[��]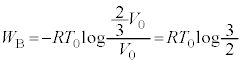 ......[��]�@����C
......[��]�@����C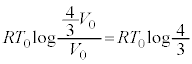 �@����E
�@����E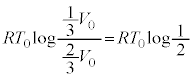 �@����F
�@����F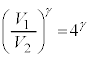 �@��
�@�� 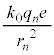 �ł��B�d�q�̑�����v�Ƃ��āA���S����
�ł��B�d�q�̑�����v�Ƃ��āA���S����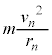 �ł��B�����̂肠�����A
�ł��B�����̂肠�����A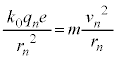 �@����@
�@����@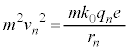 �@����A
�@����A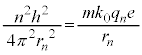 �@��
�@�� 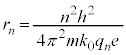 �@����B�@(�{�[�A�̌��q�͌^���Q��)
�@����B�@(�{�[�A�̌��q�͌^���Q��)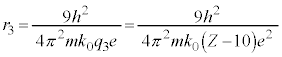 ......[��]
......[��]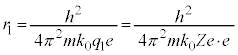
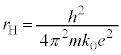 �@����D
�@����D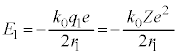
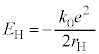 �@����E
�@����E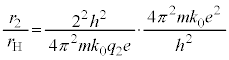
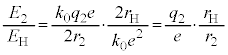
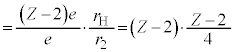
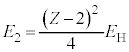 ......[��]
......[��]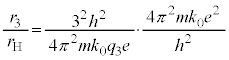
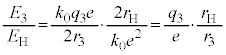
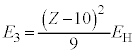 ......[��]
......[��]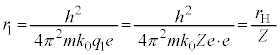 (�� �D)
(�� �D)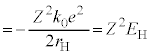 (�� �E)
(�� �E)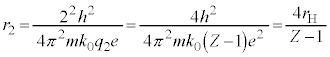 (�� �B�C�D)
(�� �B�C�D)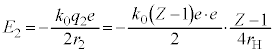
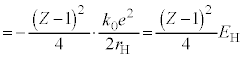
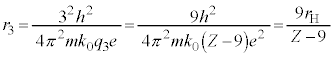 (�� �B)
(�� �B)