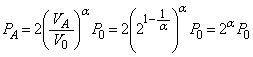���啨��'13�N[3]
���̕��͂�ǂ�ŁA�@�@�ɓK���������l���A{�@�@}����͓K�Ȃ��̂�I�т��̔ԍ����A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ������̂�\���B�܂��A��1�C��2�ɂ��ẮA�w���ɂ��������āA�����ꂼ��̉��ɋL������B
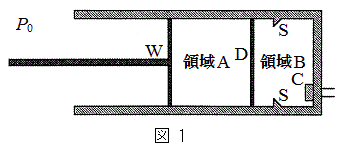 �}1�Ɏ����悤�ɁA�s�X�g��W�Ǝd�ؔ�D�ɂ���ē����̗̈����ꂽ�V�����_�[������B�V�����_�[�͌Œ肳��Ă���A�s�X�g��W�Ǝd�ؔ�D�͖��C�Ȃ��ɓ������Ƃ��ł���B�s�X�g��W�Ǝd�ؔ�D�̊Ԃ�̈�A�Ƃ��A�d�ؔ�D�ƃV�����_�[�E�[�̊Ԃ�̈�B�Ƃ���B�̈�A�Ɨ̈�B�ɂ́A�قȂ闝�z�C�̂����ꂼ�ꖧ����Ă���B��σ�����M��
�}1�Ɏ����悤�ɁA�s�X�g��W�Ǝd�ؔ�D�ɂ���ē����̗̈����ꂽ�V�����_�[������B�V�����_�[�͌Œ肳��Ă���A�s�X�g��W�Ǝd�ؔ�D�͖��C�Ȃ��ɓ������Ƃ��ł���B�s�X�g��W�Ǝd�ؔ�D�̊Ԃ�̈�A�Ƃ��A�d�ؔ�D�ƃV�����_�[�E�[�̊Ԃ�̈�B�Ƃ���B�̈�A�Ɨ̈�B�ɂ́A�قȂ闝�z�C�̂����ꂼ�ꖧ����Ă���B��σ�����M��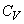 �C�C�̒萔��R�Ƃ���ƁA�̈�A�Ɨ̈�B�ɖ����Ă���C�̂�
�C�C�̒萔��R�Ƃ���ƁA�̈�A�Ɨ̈�B�ɖ����Ă���C�̂�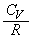 �̒l�́A���ꂼ��
�̒l�́A���ꂼ��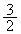 ��
��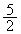 �ł���B�V�����_�[�̊O�ǂƃs�X�g���C�d�ؔ́A���ׂĒf�M�ނłł��Ă���B�̈�B�̋C�̂́A�V�����_�[�̉E�[�Ɏ��t����ꂽ���x���ߊ�C�ɂ���ĉ��M�܂��͗�p�����B�̈�B�̋C�̑S�̂̉��x�́A���݂₩�ɉ��x���ߊ�̐ݒ艷�x�ɂȂ���̂Ƃ���B�Ȃ��A���x���ߊ�̓d�����ƁA�̈�B�͒f�M���ƂȂ�B����ɁA�V�����_�[�����ɂ̓X�g�b�p�[S���݂����Ă���A�d�ؔ��X�g�b�p�[���E���ɓ������Ƃ͂Ȃ��B�d�ؔ��X�g�b�p�[�̈ʒu�ɂ���Ƃ��̗̈�B�̑̐ς�
�ł���B�V�����_�[�̊O�ǂƃs�X�g���C�d�ؔ́A���ׂĒf�M�ނłł��Ă���B�̈�B�̋C�̂́A�V�����_�[�̉E�[�Ɏ��t����ꂽ���x���ߊ�C�ɂ���ĉ��M�܂��͗�p�����B�̈�B�̋C�̑S�̂̉��x�́A���݂₩�ɉ��x���ߊ�̐ݒ艷�x�ɂȂ���̂Ƃ���B�Ȃ��A���x���ߊ�̓d�����ƁA�̈�B�͒f�M���ƂȂ�B����ɁA�V�����_�[�����ɂ̓X�g�b�p�[S���݂����Ă���A�d�ؔ��X�g�b�p�[���E���ɓ������Ƃ͂Ȃ��B�d�ؔ��X�g�b�p�[�̈ʒu�ɂ���Ƃ��̗̈�B�̑̐ς�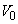 �ł���B�s�X�g���A�d�ؔA�X�g�b�p�[�A���x���ߊ�̑̐ς͖����ł�����̂Ƃ���B�܂��A�s�X�g���̍����͏�ɑ�C���ƂȂ��Ă���A���̒l��
�ł���B�s�X�g���A�d�ؔA�X�g�b�p�[�A���x���ߊ�̑̐ς͖����ł�����̂Ƃ���B�܂��A�s�X�g���̍����͏�ɑ�C���ƂȂ��Ă���A���̒l��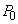 �ł���B
�ł���B
�ŏ��A�̈�A�̋C�̂̈��́A�̐ρA���x�́A���ꂼ��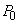 �C
�C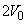 �C
�C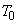 �ł���A�̈�B�̋C�̂̈��́A�̐ρA���x�́A���ꂼ��
�ł���A�̈�B�̋C�̂̈��́A�̐ρA���x�́A���ꂼ��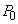 �C
�C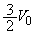 �C
�C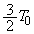 �ł������B���̏�Ԃ�������ԂƂ���B���̂Ƃ��̈�A�̋C�̂ƁA�̈�B�̋C�̂̃������͂��ꂼ��A�@���@���@���@�ł���B������Ԃ���ȉ���(1)�`(4)�Ɏ���������s�����B
�ł������B���̏�Ԃ�������ԂƂ���B���̂Ƃ��̈�A�̋C�̂ƁA�̈�B�̋C�̂̃������͂��ꂼ��A�@���@���@���@�ł���B������Ԃ���ȉ���(1)�`(4)�Ɏ���������s�����B
(1) ���x���ߊ�ŗ̈�B�̋C�̂����M���A���x��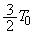 ����
����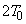 �܂ł������Ə㏸�������B���̂Ƃ��A�̈�B�̋C�̂̓����G�l���M�[�̕ω����@���@�ł���A�̈�B�̋C�̂������d�����@���@�ł��邩��A�̈�B�̋C�̂����x���ߊ킩��z�������M�ʂ��@���@�ł���B
�܂ł������Ə㏸�������B���̂Ƃ��A�̈�B�̋C�̂̓����G�l���M�[�̕ω����@���@�ł���A�̈�B�̋C�̂������d�����@���@�ł��邩��A�̈�B�̋C�̂����x���ߊ킩��z�������M�ʂ��@���@�ł���B
���z�C�̂̒f�M�ω��ł́A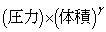 �͈��ł���B������γ�͔�M��ƌĂ�A�舳������M��
�͈��ł���B������γ�͔�M��ƌĂ�A�舳������M��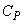 �Ƃ���ƁA
�Ƃ���ƁA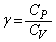 �Œ�`�����B���z�C�̂ł́A
�Œ�`�����B���z�C�̂ł́A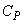 ��
��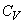 �̍�
�̍�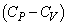 ���@���@�ɓ��������Ƃ��l������A�̈�A�̋C�̂̔�M����@���@�ł���A�̈�B�̋C�̂̔�M����@���@�ł���B
���@���@�ɓ��������Ƃ��l������A�̈�A�̋C�̂̔�M����@���@�ł���A�̈�B�̋C�̂̔�M����@���@�ł���B
�Ȃ��A�ȉ��̉ł́A�̈�A�̔�M���@���@��α�C�̈�B�̋C�̂̔�M���@���@��β �ƕ\�L����B
(2) (1)�ōs��������Ɉ��������A���x���ߊ�ŗ̈�B�̋C�̂̉��x��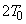 �ɕۂ��Ȃ���A�s�X�g��W�ɊO�͂������A�������ƉE���։�������ł������B�d�ؔ�D���X�g�b�p�[S�ɐڐG�����Ƃ��A�s�X�g��W���������ޑ���𒆒f���A���̂܂܂̏�Ԃŕێ������B���̂Ƃ��̈�A�̋C�̂̑̐ς��@���@�ł���B
�ɕۂ��Ȃ���A�s�X�g��W�ɊO�͂������A�������ƉE���։�������ł������B�d�ؔ�D���X�g�b�p�[S�ɐڐG�����Ƃ��A�s�X�g��W���������ޑ���𒆒f���A���̂܂܂̏�Ԃŕێ������B���̂Ƃ��̈�A�̋C�̂̑̐ς��@���@�ł���B ��1�@(2)�ōs��������ŁA�O�͂��C�̂ɂ����d�������߂�B�������A�̈�B�̋C�̂����x���ߊ��ʂ��ĊO���ɕ��o�����M�ʂ�Q�Ƃ���B���o�̉ߒ������킹�Ď����B
(3) (2)�ōs��������Ɉ��������A����Ƀs�X�g��W����������ł����ƁA�̈�A�̋C�̂̑̐ς�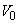 �ƂȂ����B���̎��_�Ńs�X�g��W���������ޑ���𒆒f���A���̂܂܂̏�Ԃŕێ������B���̂Ƃ��A�̈�A�̋C�̂̈��͂��@���@�ł���B
�ƂȂ����B���̎��_�Ńs�X�g��W���������ޑ���𒆒f���A���̂܂܂̏�Ԃŕێ������B���̂Ƃ��A�̈�A�̋C�̂̈��͂��@���@�ł���B ��2�@(2)�ōs��������̊J�n����(3)�ōs��������̏I���܂ł̊Ԃɂ����āA�̈�A�̋C�̂Ɨ̈�B�̋C�̂̏�ԕω����A������̐ρA�c�������͂Ƃ��Đ}������B�܂��A�̈�B�̋C�̂����ꂽ�d���ɑ�������̈��}���Ɏΐ��Ŏ����B�������A�e����̉ߒ��ŏ�Ԃ̕ω�������Ƃ��́A�ω��̐i�ޕ����ɖ���t���A���̕ω��̎n��ԂƏI��Ԃɂ�����̐ςƈ��͂�}���ɋL������B
(4) (3)�̑���Ɉ��������A���x���ߊ�ŗ̈�B�̋C�̂����M�����B�d�ؔ�D ���X�g�b�p�[���痣�ꂩ�����u�Ԃɉ��x���ߊ�̓d�����A�̈�B��f�M���Ƃ����B���̌�A�̈�A�̋C�̂̈��͂���C��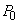 �ɓ������Ȃ�܂ŁA�������ƃs�X�g��W�������Ɉړ��������B���̂Ƃ��A�̈�B�̋C�̂̑̐ς��@���@�ł���A���̂Ƃ��̗̈�A�̋C�̂̑̐�{���F�@���傫���@�A��菬�����@�B�Ɠ�����}�B�܂��A���̉ߒ��ŗ̈�A�̋C�̂̂����d���́A�̈�B�̋C�̂̂����d��{���F�@���傫���@�A��菬�����@�B�Ɠ�����}�B�C�̂̎d���Ɋւ��邱�̂悤�Ȑ����́A�M�@�ւɂ�����������l�����ŏd�v�ł���B
�ɓ������Ȃ�܂ŁA�������ƃs�X�g��W�������Ɉړ��������B���̂Ƃ��A�̈�B�̋C�̂̑̐ς��@���@�ł���A���̂Ƃ��̗̈�A�̋C�̂̑̐�{���F�@���傫���@�A��菬�����@�B�Ɠ�����}�B�܂��A���̉ߒ��ŗ̈�A�̋C�̂̂����d���́A�̈�B�̋C�̂̂����d��{���F�@���傫���@�A��菬�����@�B�Ɠ�����}�B�C�̂̎d���Ɋւ��邱�̂悤�Ȑ����́A�M�@�ւɂ�����������l�����ŏd�v�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��M�䂪�Ⴄ�ƒf�M�ω���p-V�}���ǂ��Ⴄ�̂��Ƃ�����|�̖��ł��B�����[�����ł����A(��)�ȍ~�͂قڐ����҃[���Ƒz�����܂��B�����ł́A��蕶��ǂ܂��ɑ�������������肾�낤�ƌ��߂��ĉ��鍋�������܂����A�{��́A�������������ł��Ȃ���Ή����Ȃ��ł��傤�B��₾����ł͂Ȃ��A��蕶���s��������ł��B
(1)�̖�蕶�ɁA���x���ߊ�ŋC��B�����M���Ă���ԁA�C��A�����x�A�܂��s�X�g����d�ؔ��ǂ����Ă����̂��̋L�q������܂���B�����ł́A��C�Ƃ̂荇�����ۂ���Ă��āA�C��A�����x�͕ω����Ȃ��A�܂�A�C��A�̏�ԕω��͂Ȃ��A�C��B���舳�ω����������̂Ƃ��ĉ��܂��B(4)��蕶��{��}�̑O�́u���̉ߒ��v���A�ǂ̉ߒ����w���̂��킩��܂��A�����ł͉��x���ߊ�̓d���������̉ߒ��Ƃ��ĉ��܂��B�������Ŏ��͂ǂ������̂ł��傤���H
��1�ł́A��C���C��A�ƋC��B���d�������Ă��邱�Ƃɒ��ӂ��܂��B
(1) �C��A�̃�������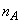 �Ƃ��āA �ŏ��̋C��A����ԕ������́A
�Ƃ��āA �ŏ��̋C��A����ԕ������́A 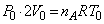 �@��
�@�� 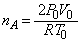
(��) 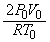 ......[��]�C��B�̃�������
......[��]�C��B�̃�������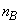 �Ƃ��āA�ŏ��̋C��B����ԕ������́A
�Ƃ��āA�ŏ��̋C��B����ԕ������́A 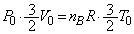 �@��
�@�� 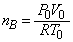
(��) 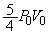 ......[��]�C��B�����M���Ă���ԁA�s�X�g���A�d�ؔɓ����͂̂荇�����������Ă��āA�C��A�C�C��B��������
......[��]�C��B�����M���Ă���ԁA�s�X�g���A�d�ؔɓ����͂̂荇�����������Ă��āA�C��A�C�C��B��������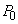 �̂܂܂ƍl���܂��B
�̂܂܂ƍl���܂��B
�C��B�̉��M�����ԕ������́A�̐���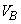 �Ƃ��āA
�Ƃ��āA (��)�̌��ʂ��A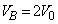
�C��B�������d���́A (��) 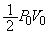 ......[��]
......[��]
(��)�A(��)�̌��ʂ��A�C��B���z�������M�́A (��) 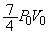 ......[��]�}�C���[�̊W�����A
......[��]�}�C���[�̊W�����A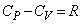 (��) R ......[��]�C��A�̔�M���
(��) R ......[��]�C��A�̔�M���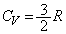 ���A
���A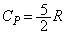 �C
�C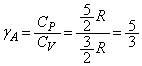 (
(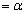 )
)
(��) 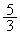 ......[��]�C��B�̔�M���
......[��]�C��B�̔�M���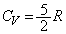 ���A
���A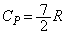 �C
�C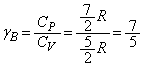 (
(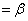 )
)
(��) 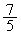 ......[��]
......[��]
(2) �s�X�g�����������ފԂ��A�d�ؔɓ����͂̂荇�����������Ă��āA�C��A�ƋC��B�������͓������Ȃ�܂��B�d�ؔ��X�g�b�p�[S�ɐڐG�������_��������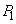 �C�C��A���̐���
�C�C��A���̐���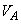 �C���x��
�C���x��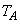 �Ƃ��āA�C��A����ԕ������́A
�Ƃ��āA�C��A����ԕ������́A 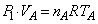 �@����@
�@����@(��)�̌��ʂ��A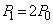
��蕶���f�M�ω��̊W��(�|�A�b�\���̊W��)���A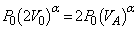
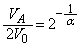 �@��
�@�� 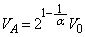
(��) 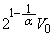 ......[��]
......[��] ��1�@�@��(��)�̌��ʂ��A
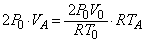 �@��
�@�� 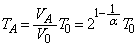
�C��A�������G�l���M�[�̕ω��́A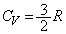 ���A(��)�̌��ʂ�p���āA
���A(��)�̌��ʂ�p���āA �C��B�́A�����ω�������̂������G�l���M�[�̕ω���0�C���o�����M����Q�ŁA�M�͊w��1�@�����A�̈�B�̋C�̂̂����d���́A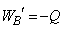
�C��A���d�ؔ�ʂ��ċC��B�ɂ����d���́A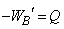
���̊Ԃ̋C��A�C��B���킹���̐ϕω��́A �s�X�g������ċC��A����C�ɍR���Ă����d�����A
�O�����C�̂ɂ����d����W�Ƃ��āA�C��A�������d���́A
�C��A���f�M�ω������Ă���̂ŁA�M�͊w��1�@�����A
�� 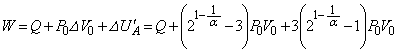
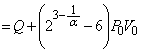 ......[��]
......[��]
(3) �����ł��C��A���f�M�ω������܂��B
�̐���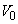 �ɂȂ����Ƃ��̋C��A��������
�ɂȂ����Ƃ��̋C��A��������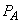 �Ƃ��āA�|�A�b�\���̊W�����A(��)�̌��ʂ�p���āA
�Ƃ��āA�|�A�b�\���̊W�����A(��)�̌��ʂ�p���āA 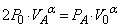 �@��
�@�� 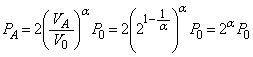
(��) 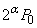 ......[��]
......[��] 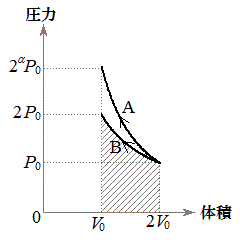 ��2�@(3)�̉ߒ��ł͎d�ؔ��X�g�b�p�[�Ŏ~�܂��Ă���̂ŋC��B�̏�Ԃ͕ω����܂���B�C��B��(2)�̉ߒ��������ω����āA
��2�@(3)�̉ߒ��ł͎d�ؔ��X�g�b�p�[�Ŏ~�܂��Ă���̂ŋC��B�̏�Ԃ͕ω����܂���B�C��B��(2)�̉ߒ��������ω����āA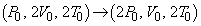 �ƕω����܂��B
�ƕω����܂��B�C��A��(2)�C(3)��ʂ����f�M�ω����A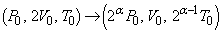 �ƕω����܂��B
�ƕω����܂��B
�����ω���p-V�}�����f�M�ω���p-V�}�̕����X�����}�ɂȂ邱�Ƃɒ��ӂ��Ă��������B
�̈�A�C�̈�B�̋C�̂̏�ԕω���}������ƉE�}(�ΐ����͗̈�B�̋C�̂����ꂽ�d��)�B�Ȃ��A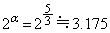 �ł��B
�ł��B
(4) ���x���ߊ�ŋC��B�����M���āA�C��A�Ɠ�������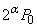 �ɂȂ����Ƃ��A�C��B���̐���
�ɂȂ����Ƃ��A�C��B���̐���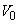 �ŁA���̌�A���x���ߊ�̓d���������́A�C��B�C�C��A�Ƃ����f�M�ω������܂��B
�ŁA���̌�A���x���ߊ�̓d���������́A�C��B�C�C��A�Ƃ����f�M�ω������܂��B �s�X�g���������ċC��A��������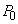 �C�]���ċC��B��������
�C�]���ċC��B��������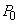 �Ƃ����Ƃ��̋C��B���̐���
�Ƃ����Ƃ��̋C��B���̐���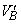 �Ƃ���ƁA�|�A�b�\���̊W�����A
�Ƃ���ƁA�|�A�b�\���̊W�����A 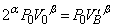 �@��
�@�� 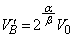
(��) 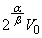 ......[��]�C��B�����M���Ă���ԁA�d�͓ؔ����Ȃ��̂ŁA�C��A�̏�Ԃ͕ω������A������
......[��]�C��B�����M���Ă���ԁA�d�͓ؔ����Ȃ��̂ŁA�C��A�̏�Ԃ͕ω������A������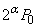 �C�̐���
�C�̐���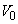 �̂܂܂ł��B
�̂܂܂ł��B
���x���ߊ�̓d���������A�C��A�C�C��B�͂Ƃ����f�M�ω������܂����A�|�A�b�\���̊W���F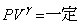 �ɂ����āA�C��B�̕�����M��γ���������̂�p-V�}�́A�C��B�̕����Ȃ��炩�ɂȂ�܂�(
�ɂ����āA�C��B�̕�����M��γ���������̂�p-V�}�́A�C��B�̕����Ȃ��炩�ɂȂ�܂�(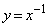 �̃O���t��
�̃O���t��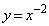 �̃O���t���ׂĂ݂Ă�������)�B
�̃O���t���ׂĂ݂Ă�������)�B
���x���ߊ�̓d����������_�ŋC��A�ƋC��B���������̐��͈�v���Ă���̂ŁA���̌㗼�C�̂��̐����������ė��҂�������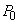 �ƂȂ����Ƃ��A�̐��͋C��B�̕����傫���Ȃ�A�C��B��p-V�}���C��A��p-V�}�̏�ɗ��܂��Bp-V�}��V���Ƃň͂��ʐ����C�̂̂����d���Ɉ�v����̂ŁA�C�̂̂����d���͋C��B�̕����傫���Ȃ�܂��B(��) �@�@(��) �A ......[��]
�ƂȂ����Ƃ��A�̐��͋C��B�̕����傫���Ȃ�A�C��B��p-V�}���C��A��p-V�}�̏�ɗ��܂��Bp-V�}��V���Ƃň͂��ʐ����C�̂̂����d���Ɉ�v����̂ŁA�C�̂̂����d���͋C��B�̕����傫���Ȃ�܂��B(��) �@�@(��) �A ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 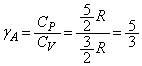 (
(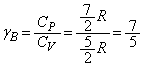 (
(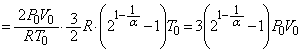
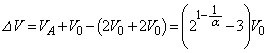
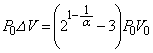
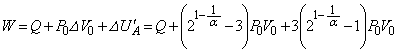
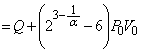 ......[��]
......[��]