����嗝�n���w'09�N���[5]
m�Cn�����R���Ƃ���Ƃ��A���̖₢�ɓ�����B
(1) ��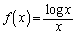 ��
��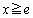 �ɂ����ĒP���Ɍ������邱�Ƃ������B
�ɂ����ĒP���Ɍ������邱�Ƃ������B (2) 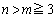 �̂Ƃ��A
�̂Ƃ��A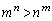 �����藧���Ƃ������B
�����藧���Ƃ������B (3) 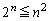 ����n�����ׂċ��߂�B
����n�����ׂċ��߂�B (4) k��2�ȏ�̎��R���Ƃ���B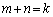 ����
����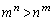 �������R���̑g
�������R���̑g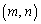 �̌�
�̌�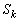 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u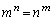 �����قȂ鎩�R���̑g
�����قȂ鎩�R���̑g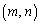 �����߂�v�Ƃ����p�o���ł���A
�����߂�v�Ƃ����p�o���ł���A
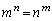 ��
�� 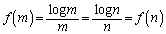
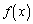 ��
��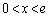 �ɂ������P�������A
�ɂ������P�������A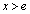 �ɂ������P�������ł��邱�Ƃ���A
�ɂ������P�������ł��邱�Ƃ���A
�ƂȂ�܂��B�{���́A����������������ł����A(4)�ׂ͍����ꍇ�������K�v�łȂ��Ȃ��ʓ|�ł��B
(1) 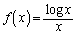
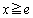 �ɂ����āA
�ɂ����āA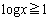 ���A
���A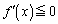
����āA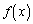 ��
��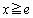 �ɂ������P�������ł��B
�ɂ������P�������ł��B
(2) 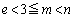 ��(1)���A
��(1)���A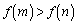
�� 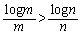
m�Cn�͎��R���Ȃ̂ŁA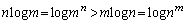 �@(�ΐ������Q��)��
�@(�ΐ������Q��)�� 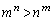
(1)���A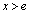 �ɂ�����
�ɂ�����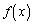 �͒P�������ł����A
�͒P�������ł����A
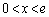 �ɂ�����
�ɂ�����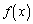 �͒P�������ł��B
�͒P�������ł��B
�]���āA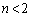 (
(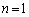 ��������܂���)�ł���A
��������܂���)�ł���A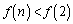
�܂��A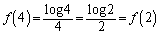 ���A
���A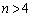 �ł���A
�ł���A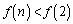
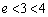 ���A
���A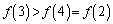
�ȏ���A�@����n�́A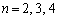 ......[��]
......[��]
(4) �܂��A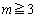 ����
����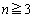 �ł���A(2)���A
�ł���A(2)���A 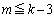 �@����B
�@����B�ƂȂ�܂����A�A���l�����āA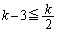 �Ƃ���ƁA
�Ƃ���ƁA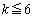 (���̂Ƃ��ɁA�A����m�͑��݂��܂���)�����ŁA
(���̂Ƃ��ɁA�A����m�͑��݂��܂���)�����ŁA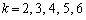 �̏ꍇ�ƁA
�̏ꍇ�ƁA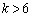 �̏ꍇ��ʂɍl���邱�Ƃɂ��܂��B
�̏ꍇ��ʂɍl���邱�Ƃɂ��܂��B
�܂��A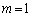 �̂Ƃ��A
�̂Ƃ��A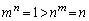 �������R��n�͑��݂��܂���B�]���āA
�������R��n�͑��݂��܂���B�]���āA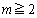 �̂ݍl����Ώ\���ł��B�@����C
�̂ݍl����Ώ\���ł��B�@����C
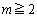 �̂Ƃ��A
�̂Ƃ��A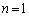 �Ƃ���ƁA
�Ƃ���ƁA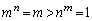 �͕K���������܂��B�@����D
�͕K���������܂��B�@����D
�܂��A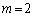 �̂Ƃ��A(3)���A
�̂Ƃ��A(3)���A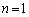 �ȊO�ɁA
�ȊO�ɁA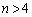 �ł���A
�ł���A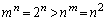 ���������܂��B����āA
���������܂��B����āA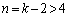 �C�܂�A
�C�܂�A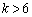 �̂Ƃ��ɂ́A�A���A
�̂Ƃ��ɂ́A�A���A 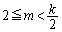 �@����E
�@����E�ł���A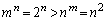 ���������܂��B
���������܂��B (i) 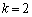 �̂Ƃ��A
�̂Ƃ��A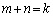 �������R���̑g
�������R���̑g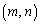 �́A
�́A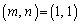 �݂̂Ȃ̂ŁA�C���A
�݂̂Ȃ̂ŁA�C���A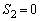
(ii) 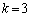 �̂Ƃ��A
�̂Ƃ��A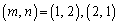 �ł����A�C�C�D���A
�ł����A�C�C�D���A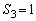
(iii) 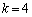 �̂Ƃ��A
�̂Ƃ��A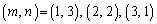 �ł����A
�ł����A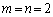 �ł́A
�ł́A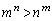 �͐��������A�C�C�D���A
�͐��������A�C�C�D���A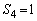
(iv) 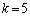 �̂Ƃ��A
�̂Ƃ��A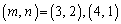 �ł���A
�ł���A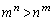 ���������A
���������A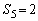
(v) 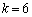 �̂Ƃ��A�A����m�����݂��Ȃ����Ƃɒ��ӂ��āA
�̂Ƃ��A�A����m�����݂��Ȃ����Ƃɒ��ӂ��āA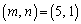 �̏ꍇ�̂݁A
�̏ꍇ�̂݁A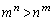 ���������A
���������A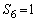
(vi) 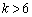 �̂Ƃ��A�B����������̂ŁA�E�����ꍇ�A�y�сA�D���
�̂Ƃ��A�B����������̂ŁA�E�����ꍇ�A�y�сA�D���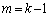 �ƂȂ�ꍇ�ɁA
�ƂȂ�ꍇ�ɁA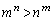 ���������܂��B�܂��A�E�ɏo�Ă���
���������܂��B�܂��A�E�ɏo�Ă���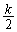 �������ɂȂ邩�ǂ����A�܂�Ak������������ŏꍇ�������܂��B
�������ɂȂ邩�ǂ����A�܂�Ak������������ŏꍇ�������܂��B (a) k����̂Ƃ��A�E �� 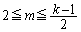 ����m�́A
����m�́A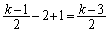 ����܂��B
����܂��B 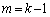 �̏ꍇ�ƍ��킹�āA
�̏ꍇ�ƍ��킹�āA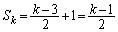 �@����F
�@����F(b) k�������̂Ƃ��A�E �� 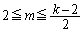 ����m�́A
����m�́A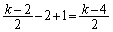 ����܂��B
����܂��B 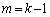 �̏ꍇ�ƍ��킹�āA
�̏ꍇ�ƍ��킹�āA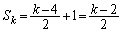 �@����G
�@����G(ii)�C(iv)��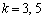 �̏ꍇ���F���������A(i)�C(iii)��
�̏ꍇ���F���������A(i)�C(iii)��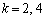 �̏ꍇ���G����������̂ŁA�ȏ���Ak����̂Ƃ�
�̏ꍇ���G����������̂ŁA�ȏ���Ak����̂Ƃ�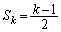 �Ck��6�ȊO�̋����̂Ƃ�
�Ck��6�ȊO�̋����̂Ƃ�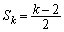 �C
�C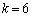 �̂Ƃ�
�̂Ƃ�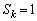 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B