��嗝�n���w'25�N�O��[5]
�������Ƃ��ɕ\�Ɨ��̏o��m�������ꂼ��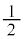 �̃R�C��������BA�CB�CC��3������BAC�̂悤��1�����ׂē����镶����ɑ��āA�R�C���𓊂��Ď��̑�����s���B
�̃R�C��������BA�CB�CC��3������BAC�̂悤��1�����ׂē����镶����ɑ��āA�R�C���𓊂��Ď��̑�����s���B
�E�\���o���當����̍�����1�����ڂ�2�����ڂ���ꂩ����B
�E�����o���當����̍�����2�����ڂ�3�����ڂ���ꂩ����B
�Ⴆ�A������BAC�ł���Ƃ��ɁA2���ăR�C���𓊂��ĕ\�A���̏��ɏo���Ƃ���ƁA�������BAC����ABC���o��ACB�ƂȂ�B
�ŏ��̕������ABC�ł���Ƃ���B�R�C����n���ē��������Ƃ̕�����ABC�ł���m����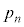 �Ƃ��ABCA�ł���m����
�Ƃ��ABCA�ł���m����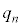 �Ƃ���B
�Ƃ���B
(1) k�𐳂̐����Ƃ���Ƃ��A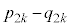 �����߂�B
�����߂�B (2) n�𐳂̐����Ƃ���Ƃ��A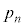 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���`�}�������Ă݂�A������ڂ���ɂ��Ă���J���N���͂���������܂��B
A�CB�CC��3��������ׂĂł��镶�����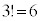 �ʂ肠��܂��B
�ʂ肠��܂��B
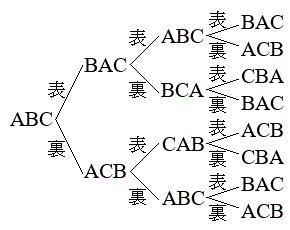 �ŏ��̕�����ABC�ł���Ƃ����Ƃ��̎��`�}���E�}�Ɏ����܂��B�E�}���A
�ŏ��̕�����ABC�ł���Ƃ����Ƃ��̎��`�}���E�}�Ɏ����܂��B�E�}���A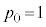 �C
�C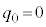 �C
�C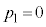 �C
�C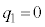 �C
�C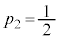 �C
�C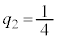 �@����@
�@����@
�E�}������ƁA������ڂɂł��镶�����ABC�CBCA�CCAB�̂ǂꂩ�ŁA���ڂɂł��镶�����BAC�CACB�CCBA�̂ǂꂩ�A�Ƃ������Ƃ�������܂��B������m�F���Ă����܂��B
������ABC�̂Ƃ��A�\���o���BAC�C�����o���ACB�ɂȂ�܂��B
������BCA�̂Ƃ��A�\���o���CBA�C�����o���BAC�ɂȂ�܂��B
������CAB�̂Ƃ��A�\���o���ACB�C�����o���CBA�ɂȂ�܂��B
�܂�A������ABC��BCA��CAB�̂Ƃ��Ɏ��ɂł��镶�����ACB��BAC��CBA�̂ǂꂩ�ł��B
������ACB�̂Ƃ��A�\���o���CAB�C�����o���ABC�ɂȂ�܂��B
������BAC�̂Ƃ��A�\���o���ABC�C�����o���BCA�ɂȂ�܂��B
������CBA�̂Ƃ��A�\���o���BCA�C�����o���CAB�ɂȂ�܂��B
�܂�A������ACB��BAC��CBA�̂Ƃ��Ɏ��ɂł��镶�����ABC��BCA��CAB�ɂȂ�܂��B
�ȏ���A�ŏ��̕�����ABC�ł���Ƃ��A������ڂɂł��镶�����ABC�CBCA�CCAB�̂ǂꂩ�ŁA���ڂɂł��镶�����BAC�CACB�CCBA�̂ǂꂩ�ł��B

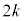 ��߂ɕ�����ABC(�m��
��߂ɕ�����ABC(�m��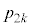 )�C���邢��BCA(�m��
)�C���邢��BCA(�m��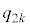 )�C���邢��CAB(�m��
)�C���邢��CAB(�m��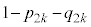 )�������Ƃ��A����2��̃R�C�������̌��ʂ̎��`�}���E�}�Ɏ����܂��B
)�������Ƃ��A����2��̃R�C�������̌��ʂ̎��`�}���E�}�Ɏ����܂��B
������A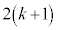 ��ڂɕ�����ABC�ɂȂ�̂́A
��ڂɕ�����ABC�ɂȂ�̂́A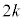 ��ڂɕ�����ABC(�m��
��ڂɕ�����ABC(�m��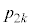 )�ŕ\�\�Əo��(�m��
)�ŕ\�\�Əo��(�m��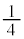 )�������Əo��(�m��
)�������Əo��(�m��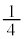 )�Ƃ��A�܂��́A
)�Ƃ��A�܂��́A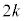 ��ڂɕ�����BCA(�m��
��ڂɕ�����BCA(�m��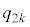 )�ŗ��\�Əo��(�m��
)�ŗ��\�Əo��(�m��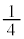 )�Ƃ��A�܂��́A
)�Ƃ��A�܂��́A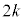 ��ڂɕ�����CAB(�m��
��ڂɕ�����CAB(�m��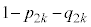 )�ŕ\���Əo��(�m��
)�ŕ\���Əo��(�m��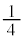 )�Ƃ��ł��B�����
)�Ƃ��ł��B�����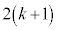 ��ڂɕ�����ABC�ƂȂ��m��
��ڂɕ�����ABC�ƂȂ��m��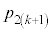 �́A
�́A
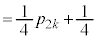 �@����A
�@����A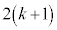 ��ڂɕ�����BCA�ɂȂ�̂́A
��ڂɕ�����BCA�ɂȂ�̂́A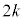 ��ڂɕ�����ABC(�m��
��ڂɕ�����ABC(�m��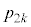 )�ŕ\���Əo��(�m��
)�ŕ\���Əo��(�m��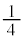 )�Ƃ��A�܂��́A
)�Ƃ��A�܂��́A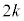 ��ڂɕ�����BCA(�m��
��ڂɕ�����BCA(�m��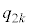 )�ŕ\�\�Əo��(�m��
)�ŕ\�\�Əo��(�m��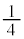 )�������Əo��(�m��
)�������Əo��(�m��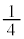 )�Ƃ��A�܂��́A
)�Ƃ��A�܂��́A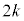 ��ڂɕ�����CAB(�m��
��ڂɕ�����CAB(�m��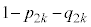 )�ŗ��\�Əo��(�m��
)�ŗ��\�Əo��(�m��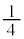 )�Ƃ��ł��B�����
)�Ƃ��ł��B�����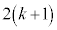 ��ڂɕ�����BCA�ƂȂ�m��
��ڂɕ�����BCA�ƂȂ�m��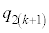 �́A
�́A
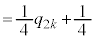 �@����B
�@����B
(1) �A�|�B���A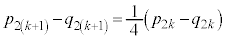
������A����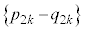 �́A�@��菉��
�́A�@��菉��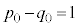 �C����
�C����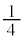 �����䐔���ł��B
�����䐔���ł��B
����āA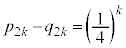 ......[��]
......[��]
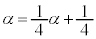 �@����C
�@����C����āA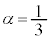
�A�|�C���A ������A����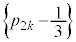 �́A�@��菉��
�́A�@��菉��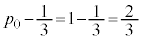 �C����
�C����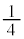 �̓��䐔��B
�̓��䐔��B
����āA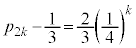 �@��
�@�� 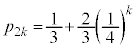 �@����Dk��0�ȏ�̐����Ƃ��āAn����A�܂�A
�@����Dk��0�ȏ�̐����Ƃ��āAn����A�܂�A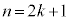 �C
�C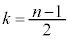 �̂Ƃ��A��L���A������ABC�ɂȂ邱�Ƃ͂Ȃ��A������ABC�ł���m����0�ł��Bn�������A�܂�A
�̂Ƃ��A��L���A������ABC�ɂȂ邱�Ƃ͂Ȃ��A������ABC�ł���m����0�ł��Bn�������A�܂�A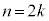 �C
�C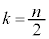 �̂Ƃ��ɂ͇D���
�̂Ƃ��ɂ͇D��� ����āAn����̂Ƃ�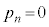 �Cn�������̂Ƃ�
�Cn�������̂Ƃ�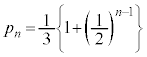 ......[��]
......[��] ���D��L�ł́A(1)��k��0�ȏ�̐����A(2)��n��0�ȏ�̐����Ƃ��ĉ��܂������A���̐����́A0�ȏ�̐����̒��Ɋ܂܂�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
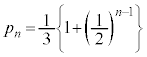 ......[��]
......[��]