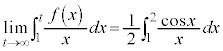大阪大学理系2025年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 平面上の三角形OABを考える。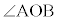 は鋭角、
は鋭角、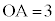 ,
,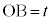 とする。また、点Aから直線OBに下ろした垂線と直線OBの交点をCとし、
とする。また、点Aから直線OBに下ろした垂線と直線OBの交点をCとし、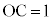 とする。線分ABを2:1に内分する点をP,点Aから直線OPに下ろした垂線と直線OBとの交点をRとする。
とする。線分ABを2:1に内分する点をP,点Aから直線OPに下ろした垂線と直線OBとの交点をRとする。
(1) 内積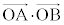 をt を用いて表せ。
をt を用いて表せ。 (2) 線分ORの長さをt を用いて表せ。
(3) 線分OBの中点をMとする。点Rが線分MB上にあるとき、t のとりうる値の範囲を求めよ。
[解答へ]
[2] pとmを実数とし、関数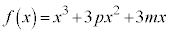 は
は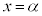 で極大値をとり、
で極大値をとり、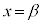 で極小値をとるとする。
で極小値をとるとする。
(1) 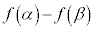 をpとmを用いて表せ。
をpとmを用いて表せ。 (2) pとmが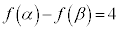 を満たしながら動くとき、曲線
を満たしながら動くとき、曲線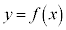 の変曲点の軌跡を求めよ。
の変曲点の軌跡を求めよ。 [解答へ]
[3] 座標空間に3点O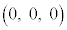 ,A
,A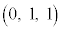 ,P
,P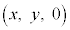 がある。
がある。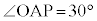 かつ
かつ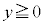 を満たすように点Pが動くとき、
を満たすように点Pが動くとき、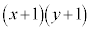 の最大値と最小値を求めよ。
の最大値と最小値を求めよ。
[解答へ]
[4] 次の問いに答えよ。
(1) 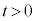 のとき
のとき が成り立つことを示せ。
(2) 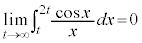 を示せ。
を示せ。 (3) 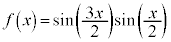 とおく。
とおく。 を示せ。
[解答へ]
[5] 投げたときに表と裏の出る確率がそれぞれ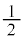 のコインがある。A,B,Cの3文字をBACのように1個ずつ並べて得られる文字列に対して、コインを投げて次の操作を行う。
のコインがある。A,B,Cの3文字をBACのように1個ずつ並べて得られる文字列に対して、コインを投げて次の操作を行う。
・表が出たら文字列の左から1文字目と2文字目を入れかえる。
・裏が出たら文字列の左から2文字目と3文字目を入れかえる。
例えば、文字列がBACであるときに、2回続けてコインを投げて表、裏の順に出たとすると、文字列はBACからABCを経てACBとなる。
最初の文字列はABCであるとする。コインをn回続けて投げたあとの文字列がABCである確率を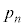 とし、BCAである確率を
とし、BCAである確率を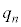 とする。
とする。
(1) kを正の整数とするとき、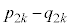 を求めよ。
を求めよ。 (2) nを正の整数とするとき、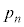 を求めよ。
を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。