ÈwåHwnw'25NOú[1]
Ö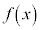 ð
ð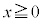 ÉεÄ
ÉεÄ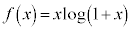 ÆèßéB
ÆèßéB
(1) sèϪ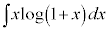 ðßæB
ðßæB (2) 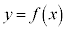 (
(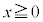 )ÌtÖð
)ÌtÖð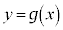 Æ·éBܽAaCbð
Æ·éBܽAaCbð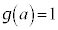 C
C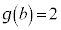 ÆÈéÀÆ·éB±ÌÆ«èϪ
ÆÈéÀÆ·éB±ÌÆ«èϪ ÌlðßæB
(3) Ö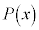 ð
ð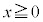 ÉεÄ
ÉεÄ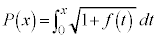 ÆèßéB
ÆèßéB
±ÌÆ«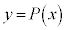 É¢ÄAè`æð
É¢ÄAè`æð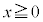 Æ·étÖ
Æ·étÖ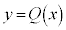 ª÷ªÂ\Å é±ÆÍؾȵÉFßÄæ¢BÖ
ª÷ªÂ\Å é±ÆÍؾȵÉFßÄæ¢BÖ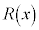 ð
ð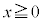 ÉεÄ
É뵀 ÆèßéÆ«A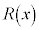 ðßæB
ðßæB
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@(3)ÍutÖvÆ¢¤±ÆŬµ»¤Å·ªA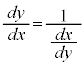 C
C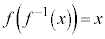 Æ¢¤±ÆÅ·B
Æ¢¤±ÆÅ·B
(2) 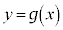 Ì
Ì 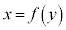 ÈÌÅA
ÈÌÅA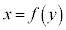 ƨÆA
ƨÆA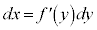 CxF
CxF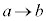 ÌÆ«A
ÌÆ«A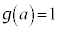 C
C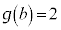 æèAyF
æèAyF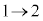 C(1)ÌÊðp¢ÄA
C(1)ÌÊðp¢ÄA 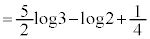 ......[]
......[]
(3) 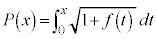 ̼ÓðxÅ÷ª·éÆA
̼ÓðxÅ÷ª·éÆA 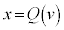 Ì
Ì 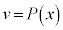 æèA
æèA±êæèA
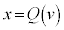 ƵÄu·Ïªðs¤ÆA
ƵÄu·Ïªðs¤ÆA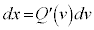 CvF
CvF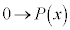 ÌÆ«A
ÌÆ«A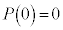 æè
æè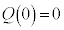 Å èA
Å èA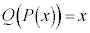 (tÖÌ«¿
(tÖÌ«¿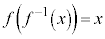 ÉÓ)æèAxF
ÉÓ)æèAxF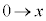 CAðp¢ÄA
CAðp¢ÄA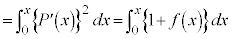 @(æ @)
@(æ @)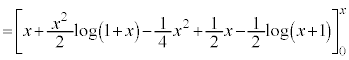 @((1)ÌÊæè)
@((1)ÌÊæè)
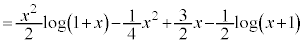 ......[]
......[]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@ÈwåwTOP@@wTOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B 
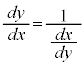 C
C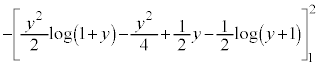
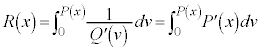
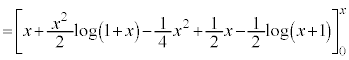 @((1)ÌÊæè)
@((1)ÌÊæè)