���嗝�n���w'18�N�O��[5]
���f�����ʏ�̌��_�𒆐S�Ƃ��锼�a1�̉~��C�Ƃ���B�_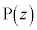 ��C��ɂ���A�_
��C��ɂ���A�_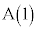 �Ƃ͈قȂ�Ƃ���B�_P�ɂ�����~C�̐ڐ��Ɋւ��āA�_A�ƑΏ̂ȓ_��
�Ƃ͈قȂ�Ƃ���B�_P�ɂ�����~C�̐ڐ��Ɋւ��āA�_A�ƑΏ̂ȓ_��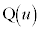 �Ƃ���B
�Ƃ���B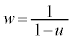 �Ƃ����Aw�Ƌ����ȕ��f����
�Ƃ����Aw�Ƌ����ȕ��f����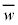 �ŕ\���B
�ŕ\���B
(1) u��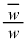 ��z�ɂ��Ă̐����Ƃ��ĕ\���A��Βl�̏�
��z�ɂ��Ă̐����Ƃ��ĕ\���A��Βl�̏�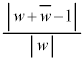 �����߂�B
�����߂�B (2) C�̂���������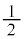 �ȉ��̕��f���ŕ\����镔����
�ȉ��̕��f���ŕ\����镔����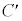 �Ƃ���B�_
�Ƃ���B�_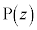 ��
��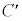 ����Ƃ��̓_
����Ƃ��̓_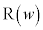 �̋O�Ղ����߂�B
�̋O�Ղ����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@ �uC�̂���������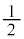 �ȉ��̕��f���ŕ\����镔���v�A�܂�A
�ȉ��̕��f���ŕ\����镔���v�A�܂�A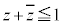 �Ƃ��������ƁAw�̒l����ǂ����ѕt���邩�A�Ƃ������Ƃɋ�J���܂��B�ȉ��ł́A�f���ɍl����hang up�ɒǂ����܂�܂����Aw�̎����ɖڂ�t����Ή��Ƃ��Ȃ�Ƃ����A���܂��܊��͂��@�����Ƃ��A2���������̗��_�̊��p�ɂ��A�O�Ղ̗L�����������߂邱�Ƃ��ł��܂��B
�Ƃ��������ƁAw�̒l����ǂ����ѕt���邩�A�Ƃ������Ƃɋ�J���܂��B�ȉ��ł́A�f���ɍl����hang up�ɒǂ����܂�܂����Aw�̎����ɖڂ�t����Ή��Ƃ��Ȃ�Ƃ����A���܂��܊��͂��@�����Ƃ��A2���������̗��_�̊��p�ɂ��A�O�Ղ̗L�����������߂邱�Ƃ��ł��܂��B
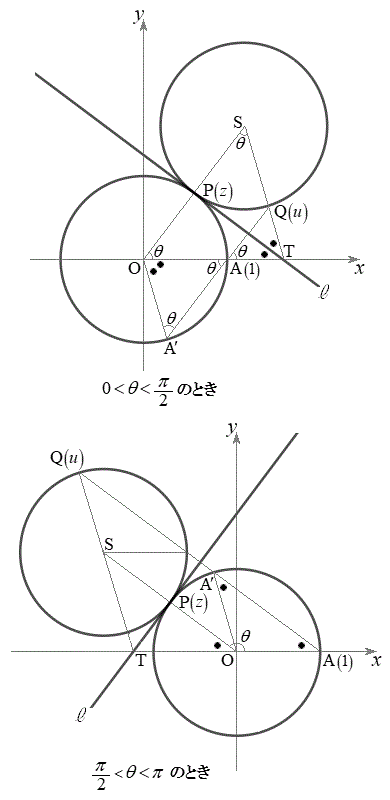 ���_��O�Ƃ��A
���_��O�Ƃ��A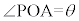 �Ƃ��܂��B
�Ƃ��܂��B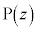 ��C��̓_��
��C��̓_��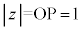 �C
�C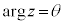 �Ȃ̂�(�Ɍ`�����Q��)�A
�Ȃ̂�(�Ɍ`�����Q��)�A
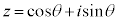 �@����@
�@����@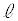 �C�ڐ�
�C�ڐ�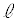 �Ɋւ��Č��_O���Ώ̂ȓ_��S�Ƃ��܂��B
�Ɋւ��Č��_O���Ώ̂ȓ_��S�Ƃ��܂��B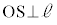 �ł���AOS�̒��_��
�ł���AOS�̒��_��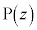 �Ȃ̂ŁAS��\�����f���́A
�Ȃ̂ŁAS��\�����f���́A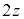 �@����A
�@����A
�ł��B
����QA�Ɖ~C�Ƃ̌�_�̂���A�łȂ����̓_��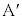 �Ƃ��܂��B
�Ƃ��܂��B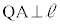 �Ȃ̂ŁAQA // OS�ł��B
�Ȃ̂ŁAQA // OS�ł��B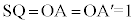 ���A�l�p�`OAQS�Ǝl�p�`
���A�l�p�`OAQS�Ǝl�p�`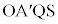 �́A���s�l�ӌ`���܂��͓��r��`�ŁA�l�p�`OAQS�����r��`�Ȃ̂ŁA�l�p�`
�́A���s�l�ӌ`���܂��͓��r��`�ŁA�l�p�`OAQS�����r��`�Ȃ̂ŁA�l�p�`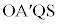 �́A���s�l�ӌ`�ł��B����āA
�́A���s�l�ӌ`�ł��B����āA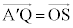 �@����B
�@����B
����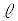 �Ǝ���(x���A����OA)�Ƃ̌�_��T�Ƃ���ƁA����OA�Ɛ���SQ�͒���
�Ǝ���(x���A����OA)�Ƃ̌�_��T�Ƃ���ƁA����OA�Ɛ���SQ�͒���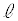 �Ɋւ��đΏ̂Ȃ̂ŁAT�͒���SQ��̓_�ł��B
�Ɋւ��đΏ̂Ȃ̂ŁAT�͒���SQ��̓_�ł��B
(1) 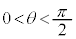 �C
�C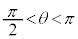 �C
�C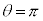 �C
�C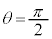 �̏ꍇ�ɕ����čl���܂��B
�̏ꍇ�ɕ����čl���܂��B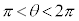 �̏ꍇ�́A
�̏ꍇ�́A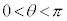 �̏ꍇ�������Ɋւ��Đ܂�Ԃ��čl����Γ��l�ł��B
�̏ꍇ�������Ɋւ��Đ܂�Ԃ��čl����Γ��l�ł��B (i) 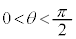 �̂Ƃ��AT��x����
�̂Ƃ��AT��x����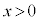 �͈̔͂ɂ���܂��B
�͈̔͂ɂ���܂��B 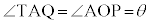 (���ʊp)�ł���A
(���ʊp)�ł���A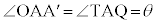 �C�܂��A��
�C�܂��A��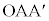 �͓ӎO�p�`�Ȃ̂ŁA
�͓ӎO�p�`�Ȃ̂ŁA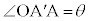 �C
�C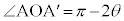 �ŁA
�ŁA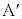 �́AA�����v����
�́AA�����v����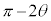 ��]�������_�A�܂�AA���v����
��]�������_�A�܂�AA���v����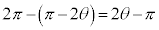 ��]�������_�ł��B����āA
��]�������_�ł��B����āA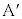 ��\�����f��α�́A�@���A
��\�����f��α�́A�@���A�A�C�B���A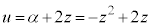
(ii) 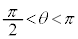 �̂Ƃ��AT��x����
�̂Ƃ��AT��x����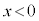 �͈̔͂ɂ���܂��B
�͈̔͂ɂ���܂��B 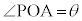 ���
���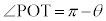 �C
�C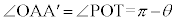 (���ʊp�AOS // AQ)�C�܂��A��
(���ʊp�AOS // AQ)�C�܂��A��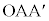 �͓ӎO�p�`�Ȃ̂ŁA
�͓ӎO�p�`�Ȃ̂ŁA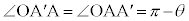
����āA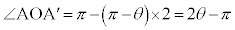 �ŁA
�ŁA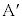 ��A���v����
��A���v����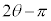 ��]�������_�ŁA(i)�Ɠ��l�ɁA
��]�������_�ŁA(i)�Ɠ��l�ɁA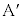 ��\�����f��α�́A
��\�����f��α�́A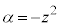 �C�B���A
�C�B���A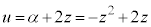
(iii)(iv)�̏ꍇ���܂߁A(i)�C(ii)�Ƃ��A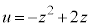 ......[��]
......[��] 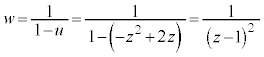 �@����C
�@����C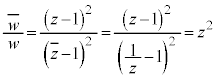 ......[��]�@(
......[��]�@(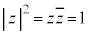 �C��Βl���Q��)
�C��Βl���Q��)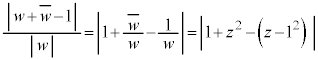
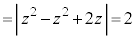 ......[��]�@(
......[��]�@(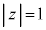 )
)
(2) (1)���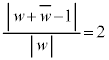 �ł����Ax�Cy�������Ƃ��āA
�ł����Ax�Cy�������Ƃ��āA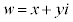 �Ƃ����A2�悵�ĕ�����A
�Ƃ����A2�悵�ĕ�����A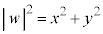 �C
�C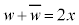 ��������ƁA
��������ƁA ������O���̕������͂킩��܂��B���́A�uC�̂���������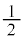 �ȉ��̕��f���ŕ\����镔���v�Ƃ��������ł��BC��̓_
�ȉ��̕��f���ŕ\����镔���v�Ƃ��������ł��BC��̓_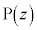 �̎�����
�̎�����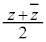 �ł��B���ꂪ
�ł��B���ꂪ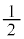 �ȉ��Ȃ̂ŁA
�ȉ��Ȃ̂ŁA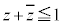 �ł��B�܂��A
�ł��B�܂��A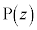 �͉~C��̓_�Ȃ̂ŁA
�͉~C��̓_�Ȃ̂ŁA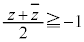 �C�܂�A
�C�܂�A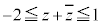 �C(1)���A
�C(1)���A ������ӁX������ƁA
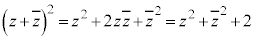 �@(
�@(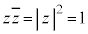 )
)���A
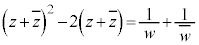 �@(�E�ӂ������ł�)
�@(�E�ӂ������ł�)�E�ӂ�W�C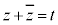 �Ƃ����ƁA
�Ƃ����ƁA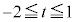 �ł����āA
�ł����āA 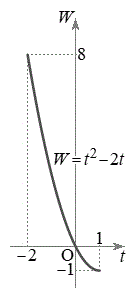 �E�}���A
�E�}���A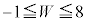 (2�����̍ő�ŏ����Q��)�C�ƂȂ肻���Ȃ̂ł����A����͂��܂��s���܂���B�E�}�őz�������Ǝv���܂����A
(2�����̍ő�ŏ����Q��)�C�ƂȂ肻���Ȃ̂ł����A����͂��܂��s���܂���B�E�}�őz�������Ǝv���܂����A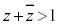 �ł����Ă��A
�ł����Ă��A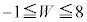 �����Ă��܂�����ł��B
�����Ă��܂�����ł��B
�Ƃ����킯�ŁA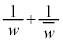 �ɒ��ڂ��Ă�z���uC�̂���������
�ɒ��ڂ��Ă�z���uC�̂���������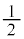 �ȉ��̕��f���ŕ\����镔���v���A�Ƃ����������l���邱�Ƃ��ł��܂���B
�ȉ��̕��f���ŕ\����镔���v���A�Ƃ����������l���邱�Ƃ��ł��܂���B
�����ŁA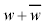 �ڍl���Ă݂܂��B(1)���A
�ڍl���Ă݂܂��B(1)���A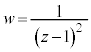 �C
�C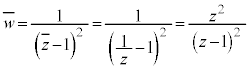
�ł��B
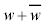 �͎����ł�(���f�����Q��)�B�����ŁAk�������Ƃ��āA
�͎����ł�(���f�����Q��)�B�����ŁAk�������Ƃ��āA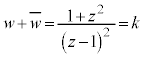 �@����E
�@����E�Ƃ����܂��B������Đ�������ƁA
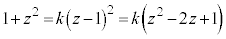
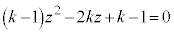 �@����F
�@����F�����z��2���������ł��B�W����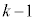 �C
�C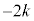 �͎����ŁA�F�͎����W����2���������Ȃ̂ŁA���̌������g���܂��Bz�ɂ��ĉ����ƁA
�͎����ŁA�F�͎����W����2���������Ȃ̂ŁA���̌������g���܂��Bz�ɂ��ĉ����ƁA 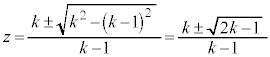 �@����G
�@����Gz���uC�̂���������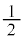 �ȉ��̕��f���ŕ\����镔���v���Ƃ��A1��������z�������ɂȂ�Ƃ��낪����܂��B
�ȉ��̕��f���ŕ\����镔���v���Ƃ��A1��������z�������ɂȂ�Ƃ��낪����܂��B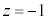 �ł��B
�ł��B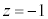 �̂Ƃ��E���
�̂Ƃ��E���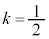 �ƂȂ�܂����A���̂Ƃ��G�̍�����(�܂蔻�ʎ�)��0�ƂȂ�A�G����������^���܂��B�ł����A
�ƂȂ�܂����A���̂Ƃ��G�̍�����(�܂蔻�ʎ�)��0�ƂȂ�A�G����������^���܂��B�ł����A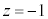 �ȊO��z�͋���(������0�łȂ����f��)�ł��B
�ȊO��z�͋���(������0�łȂ����f��)�ł��B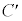 ��
��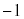 �ȊO�̓_�ł́A�G�̍������͕��ł��B����āA
�ȊO�̓_�ł́A�G�̍������͕��ł��B����āA 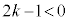 �C�����A
�C�����A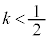 �@����H
�@����H���̂Ƃ��Az�̎�����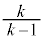 �ł��Bz�̎�����
�ł��Bz�̎�����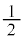 �ȉ��Ȃ̂ŁA
�ȉ��Ȃ̂ŁA 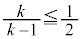 �C�����A�H(
�C�����A�H(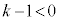 �ł�)�ɒ��ӂ��āA
�ł�)�ɒ��ӂ��āA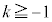 �@����I
�@����I�t�ɇH���I�ł���Az�̕������F�̉��́A�u������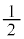 �ȉ��̋����v��^���܂��B
�ȉ��̋����v��^���܂��B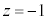 �̂Ƃ���
�̂Ƃ���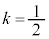 ���܂߁A�E�C�H�C�I���Aw�̎���
���܂߁A�E�C�H�C�I���Aw�̎���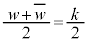 �ɂ��āA
�ɂ��āA 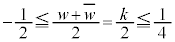 �@����J
�@����J�ƂȂ�܂��B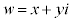 �Ƃ��āA
�Ƃ��āA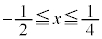 �ł��B
�ł��B
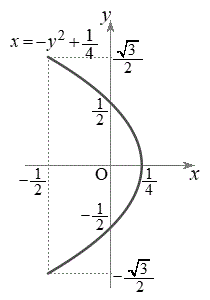 �D�C�J���A���߂�
�D�C�J���A���߂�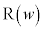 �̋O�Ղ́A������
�̋O�Ղ́A������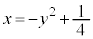 ��
��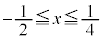 �̕��� ......[��]�C
�̕��� ......[��]�C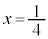 �̂Ƃ�
�̂Ƃ�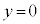 �C
�C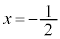 �̂Ƃ�
�̂Ƃ�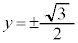 �C��������y����
�C��������y����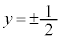 �Ō����܂��B�O�Ղ�}������ƁA�E�}�����B
�Ō����܂��B�O�Ղ�}������ƁA�E�}�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 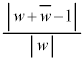 �����߂�B
�����߂�B �ł����Ax�Cy�������Ƃ��āA
�ł����Ax�Cy�������Ƃ��āA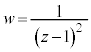 �C
�C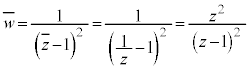
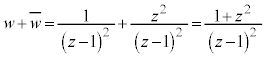
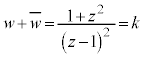 �@����E
�@����E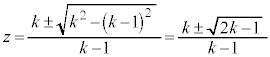 �@����G
�@����G