���嗝�n���w'25�N�O��[2]
(1) 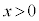 �̂Ƃ��A�s����
�̂Ƃ��A�s����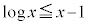 �������B
�������B
(2) ���̋Ɍ������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�́A�͂��݂����Ɏ������ނ̂��낤�A���̍ۂ�(1)���g���̂��낤�A�Ƃ����\���͗����܂����A�t���ɋ��ޑ����������̂ɋ�J���܂��B
(1) 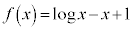 �Ƃ����܂��B
�Ƃ����܂��B
(2) �ϕ���Ԃ�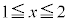 �ł��B���̂Ƃ�
�ł��B���̂Ƃ�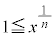 �C
�C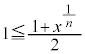 �ł���A(1)�̕s������p���āA
�ł���A(1)�̕s������p���āA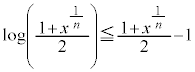
����āA
�@��n�������āA
�E�ӂ͇A���A
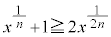 �ł������悤�ɕό`���āA
�ł������悤�ɕό`���āA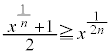
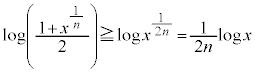 �@����B
�@����B����āA�B��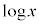 �Ƃ���ƁA
�Ƃ���ƁA 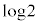 �@����C
�@����C�����ŁA�͂��݂����ɂ���Ƃ��̏����������l���܂��B
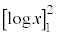 ���A
���A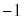
����āA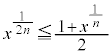 �@����D
�@����D 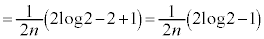 �@����E
�@����E�@�C�C�C�D�C�E���A
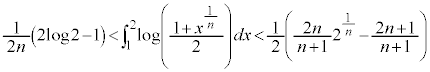 �@����F
�@����F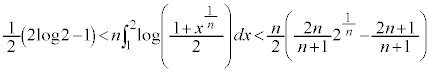 ......[��]
......[��]���D�������ŁA�@�́A(1)�𗘗p����̂��낤�Ǝv���A�����ɋC�Â���Ǝv���܂��B�m�̎��Ƃł�������ł����ƌ���������ł����A��������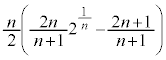 �ɂǂ�����ċC�Â����A�Ƃ������Ƃ��{��̃|�C���g�ł��B
�ɂǂ�����ċC�Â����A�Ƃ������Ƃ��{��̃|�C���g�ł��B �@����B���v�Z���A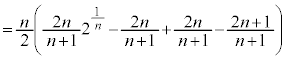 �Ƃ����Ɍ��ׂ�ƁA
�Ƃ����Ɍ��ׂ�ƁA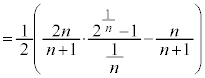 �ɂȂ�܂��B�]���āA�͂��݂����̏���������
�ɂȂ�܂��B�]���āA�͂��݂����̏���������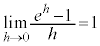 �ɂȂ�K�v������܂��B���R�A�ϕ��̌��ʂ�
�ɂȂ�K�v������܂��B���R�A�ϕ��̌��ʂ�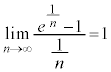 ���o�Ă��Ȃ��Ƃ����܂���B
���o�Ă��Ȃ��Ƃ����܂���B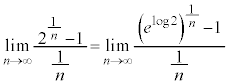 ���o�Ă���̂�
���o�Ă���̂�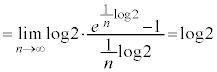 ���o�Ă���͂��ł��B�c���
���o�Ă���͂��ł��B�c���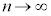 ��
��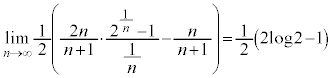 �Ƃ��ĂЂ˂�o�����ƂɋC�Â���A���������̐ϕ���
�Ƃ��ĂЂ˂�o�����ƂɋC�Â���A���������̐ϕ���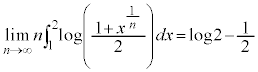 �ƂȂ��Ă���悢���낤�A�Ƃ������ƂɂȂ�܂��B����ŁA���������̕s�����́A
�ƂȂ��Ă���悢���낤�A�Ƃ������ƂɂȂ�܂��B����ŁA���������̕s�����́A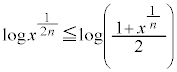 �C�܂�A
�C�܂�A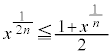 �ł���悢�A�Ƃ������ƂɂȂ�܂��B
�ł���悢�A�Ƃ������ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 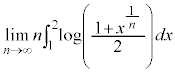
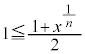 �ł���A(1)�̕s������p���āA
�ł���A(1)�̕s������p���āA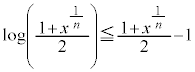
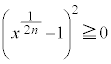
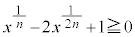
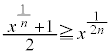
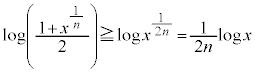 �@����B
�@����B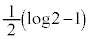
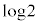 �@����C
�@����C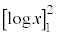 ���A
���A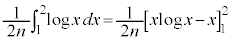 �C
�C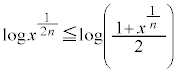
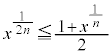 �@����D
�@����D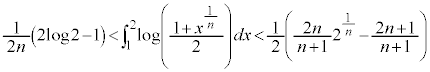 �@����F
�@����F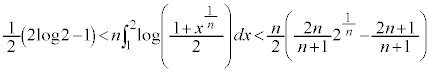 ......[��]
......[��]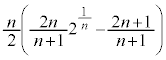 �ɂǂ�����ċC�Â����A�Ƃ������Ƃ��{��̃|�C���g�ł��B
�ɂǂ�����ċC�Â����A�Ƃ������Ƃ��{��̃|�C���g�ł��B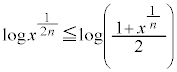 �C�܂�A
�C�܂�A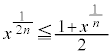 �ł���悢�A�Ƃ������ƂɂȂ�܂��B
�ł���悢�A�Ƃ������ƂɂȂ�܂��B