���啨��'18�N�O��[1]
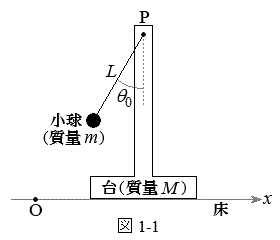
�}1-1�̂悤�ɐ����ȏ��̏�Ɏ���M�̑䂪����B��̒����ɂ͒�������A���㕔�̓_P�Ɏ���m�̏�����L�̐L�яk�݂��Ȃ����Œ݂邵���U��q�����t�����Ă���B���ɌŒ肳�ꂽx�����Ƃ�A�_O�����_�A���������E�����𐳂̌����Ƃ���B�����Ǝ��́A���⏰�ɐڐG���邱�ƂȂ�x�����܂މ����ʓ����^��������̂Ƃ���B�܂��A���Ƒ�̊Ԃɖ��C�͂Ȃ��A��͌X�����ƂȂ�x�������ɉ^��������̂Ƃ���B�ȉ��̐ݖ�ɓ�����B�������A�d�͉����x�̑傫����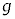 �Ƃ��A�����̑傫���A���̎��ʁA����ы�C��R�͖����ł���Ƃ���B
�Ƃ��A�����̑傫���A���̎��ʁA����ы�C��R�͖����ł���Ƃ���B
 �T�@�}1-1�̂悤�ɁA�U��q�̎�������܂Ȃ��悤�ɏ�����������������p�x
�T�@�}1-1�̂悤�ɁA�U��q�̎�������܂Ȃ��悤�ɏ�����������������p�x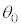 (
(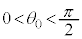 )�̈ʒu�܂Ŏ����グ�A��Ə������Î~������Ԃ���Â��Ɏ��������Ƃ���A��Ə����͐U�����Ȃ���^�������B
)�̈ʒu�܂Ŏ����グ�A��Ə������Î~������Ԃ���Â��Ɏ��������Ƃ���A��Ə����͐U�����Ȃ���^�������B(1) �������ŏ��ɍʼn��_��ʉ߂���Ƃ��́A�����̑��x��x���������߂�B
(2) ���鎞���ɂ������̑��x��x������V�C�����̑��x��x������v�Ƃ���B���̂Ƃ��A�_P���狗��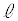 �������ꂽ����̓_�̑��x��x�������AV�Cv�C
�������ꂽ����̓_�̑��x��x�������AV�Cv�C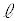 �CL��p���ĕ\���B
�CL��p���ĕ\���B (3) �_P����̋�����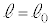 �̎���̓_Q�́Ax�������ɂ͉^�����Ȃ��B
�̎���̓_Q�́Ax�������ɂ͉^�����Ȃ��B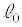 ���AM�Cm�CL��p���ĕ\���B
���AM�Cm�CL��p���ĕ\���B (4) �p�x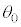 ���\���������ꍇ�̑�Ə����̉^�����l����B���̉^���̎���
���\���������ꍇ�̑�Ə����̉^�����l����B���̉^���̎���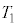 �́A�_Q���猩�������̉^�����l�@���邱�Ƃŋ��߂邱�Ƃ��ł���B����
�́A�_Q���猩�������̉^�����l�@���邱�Ƃŋ��߂邱�Ƃ��ł���B����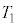 ���AM�Cm�C
���AM�Cm�C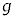 �CL��p���ĕ\���B�������A
�CL��p���ĕ\���B�������A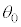 ���\���ɏ��������߁A�_Q�̉��������̉^���͖����ł���Ƃ���B�܂��A
���\���ɏ��������߁A�_Q�̉��������̉^���͖����ł���Ƃ���B�܂��A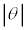 ���\���������Ƃ��ɐ��藧�ߎ����A
���\���������Ƃ��ɐ��藧�ߎ����A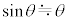 ��p���Ă悢�B
��p���Ă悢�B
 �U�@����
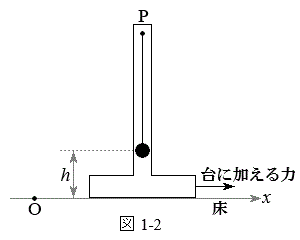
�U�@����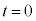 �ő�Ə������Î~���A�U��q�������������������Ă���B���̂Ƃ��A�����͏�����̍���h�̈ʒu�ɂ���B���̏�Ԃ���}1-2�̂悤�ɁA����
�ő�Ə������Î~���A�U��q�������������������Ă���B���̂Ƃ��A�����͏�����̍���h�̈ʒu�ɂ���B���̏�Ԃ���}1-2�̂悤�ɁA����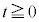 �ő䂪�����xa (
�ő䂪�����xa (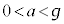 )��x���̐��̌����ɓ������x�^������悤�ɁA��ɗ�
)��x���̐��̌����ɓ������x�^������悤�ɁA��ɗ�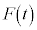 �������������B���̌��ʁA����
�������������B���̌��ʁA����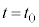 �ŁA�����̍������͂��߂čő�ƂȂ����B
�ŁA�����̍������͂��߂čő�ƂȂ����B(1) ����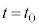 �ł̏����̍������AL�Ch�C
�ł̏����̍������AL�Ch�C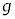 �Ca��p���ĕ\���B
�Ca��p���ĕ\���B 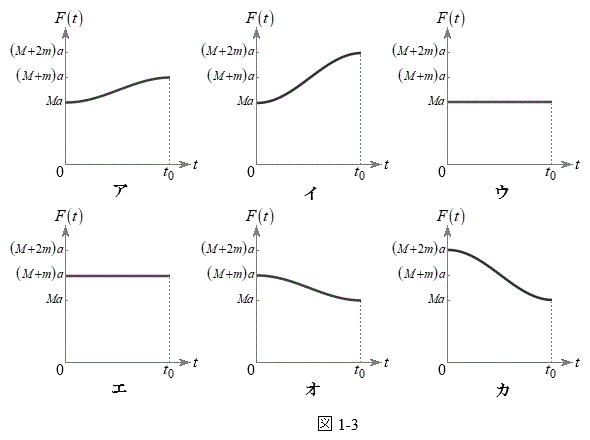 (3) ��ɉ�������
(3) ��ɉ�������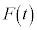 �̃O���t�Ƃ��čł��K�Ȃ��̂��A�}1-3�̃A�`�J�����I��œ�����B
�̃O���t�Ƃ��čł��K�Ȃ��̂��A�}1-3�̃A�`�J�����I��œ�����B(4) ����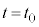 �ŁA��ɗ͂�������̂��~�߂��Ƃ���A��Ə����͂��̌���^���𑱂����B����
�ŁA��ɗ͂�������̂��~�߂��Ƃ���A��Ə����͂��̌���^���𑱂����B����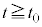 �ɂ����鎅��̓_Q�̑��x��x���������߂�B�܂��Aa��
�ɂ����鎅��̓_Q�̑��x��x���������߂�B�܂��Aa��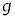 �ɔ�ׂď\���ɏ������Ƃ��A����
�ɔ�ׂď\���ɏ������Ƃ��A����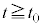 �ɂ�����_Q���猩�������̐U���̎���
�ɂ�����_Q���猩�������̐U���̎���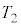 ���AM�Cm�C
���AM�Cm�C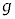 �CL��p���ĕ\���B�������A
�CL��p���ĕ\���B�������A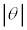 ���\���������Ƃ��ɐ��藧�ߎ����A
���\���������Ƃ��ɐ��藧�ߎ����A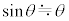 ��p���Ă悢�B
��p���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�Ɂu�L�яk�݂��Ȃ����v�Ƃ���̂ŁA�^�����s���Ă���ԁA���͂���ނ��ƂȂ��������ێ�����A�Ƃ��čl���܂��B�{��ł͇U�ŏ����猩�ė͊w�I�G�l���M�[�ۑ��̎��𗧂Ă�ꂸ�Y�݂܂��B
�T(1) �������ʼn��_��ʉ߂���Ƃ��̏����A��̑��x��x������v�CV�Ƃ��܂��B�����Ƒ䂩��Ȃ�n�ɂ�����A������������Ƃ��Ə������ʼn��_��ʉ߂���Ƃ��Ƃ�x�������^���ʕۑ����A 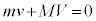 �@����@
�@����@������������Ƃ��A�ʼn��_���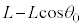 ���������ʒu�ɂ���܂��B������������Ƃ��Ə������ʼn��_��ʉ߂���Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A
���������ʒu�ɂ���܂��B������������Ƃ��Ə������ʼn��_��ʉ߂���Ƃ��Ƃ��͊w�I�G�l���M�[�ۑ����A 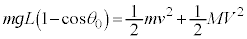 �@����A
�@����A�@���A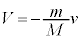 �@����B
�@����B
�A�֑������ƁA �� 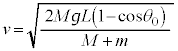 ......[��]
......[��]
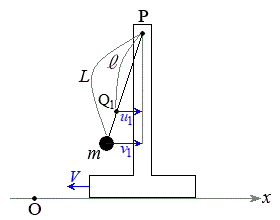 (2) �_P���狗��
(2) �_P���狗��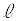 �������ꂽ����̓_
�������ꂽ����̓_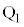 �C�����A�̑��Ō������x��x������
�C�����A�̑��Ō������x��x������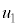 �C
�C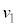 �Ƃ��܂��B�����������ێ�����ƍl���A�E�}���O�p�`�̑�������l���āA
�Ƃ��܂��B�����������ێ�����ƍl���A�E�}���O�p�`�̑�������l���āA�����猩���A�_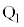 �C�����A��̑��x��x������u�Cv�CV�Ƃ���ƁA�_
�C�����A��̑��x��x������u�Cv�CV�Ƃ���ƁA�_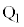 �Ə����̑��Ō������Α��x�́A
�Ə����̑��Ō������Α��x�́A 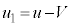 �C
�C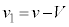
(3) (2)�̌��ʂŁA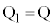 �̂Ƃ�
�̂Ƃ�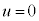 �C
�C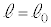 �Ƃ��āA
�Ƃ��āA ����āA�B��p���āA
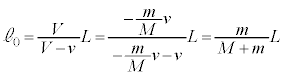 ......[��]
......[��]���D�_Q�́A����L�̎���P������m�FM�ɓ�������_�ŁA���̗��[�Ɏ���M�Cm�̕��̂��ʒu����(P����M)�Ƃ����Ƃ����d�S�ł��B
(4) �_Q�Ə����Ƃ̋����́A
�ł��B���Ɖ��������Ƃ̂Ȃ��p��θ�Ƃ���ƁA�����ɓ����d�͂̉^�������ɐ����Ȑ���f �̑傫���́A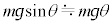 �ł��B�_Q���猩�āA������x�����̕ψ�x�́A
�ł��B�_Q���猩�āA������x�����̕ψ�x�́A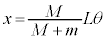 (��ʊp���Q��)�ł���A
(��ʊp���Q��)�ł���A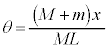 �ł��B�_Q�̉��������̉^�������āA
�ł��B�_Q�̉��������̉^�������āA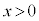 �̂Ƃ�
�̂Ƃ�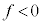 ���A�����̉^���������́A�����̉����x��a�Ƃ��āA
���A�����̉^���������́A�����̉����x��a�Ƃ��āA ���̉^���́A�P�U���ł��B���̊p�U������ω�Ƃ���ƁA�����F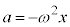 ���A
���A ����āA���̉^���̎���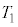 �́A
�́A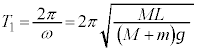 ......[��]
......[��]
�U(1) �����̍������ő�ɂȂ����Ƃ��A�܂�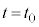 �ɂ����āA���Ō��Ď��Ɖ��������̂Ȃ��p��θ������(�����猩�Ă�θ�ł�)�Ƃ��܂��B�����̍������ő�ɂȂ����Ƃ��A�����͑�ɑ��ĐÎ~���Ă���A���Ō��āA
�ɂ����āA���Ō��Ď��Ɖ��������̂Ȃ��p��θ������(�����猩�Ă�θ�ł�)�Ƃ��܂��B�����̍������ő�ɂȂ����Ƃ��A�����͑�ɑ��ĐÎ~���Ă���A���Ō��āA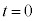 ����
����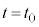 �܂ł̊ԂɁA�����͐���������
�܂ł̊ԂɁA�����͐���������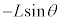 �ψʂ��Ă��܂��B���Ō����͊w�I�G�l���M�[�ۑ����l���܂��B
�ψʂ��Ă��܂��B���Ō����͊w�I�G�l���M�[�ۑ����l���܂��B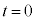 �ɂ����Ă�
�ɂ����Ă�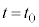 �ɂ����Ă��^���G�l���M�[��0�ŁAX����������������
�ɂ����Ă��^���G�l���M�[��0�ŁAX����������������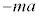 �̂����d��
�̂����d��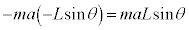 �ɂ���āA�������ʒu�G�l���M�[
�ɂ���āA�������ʒu�G�l���M�[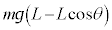 �����������ƍl����ƁA
�����������ƍl����ƁA 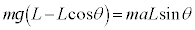 �@����C
�@����C�����ŁA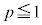 �Ȃ̂ŁA
�Ȃ̂ŁA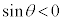 �Ƃ������Ƃ͂Ȃ��A
�Ƃ������Ƃ͂Ȃ��A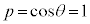 �Ƃ����������݂���(
�Ƃ����������݂���(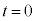 �C����
�C����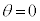 �̂Ƃ��ɂ��C�͐������܂�)���Ƃɒ��ӂ��Ă��������B���ӂ�2�悵�āA
�̂Ƃ��ɂ��C�͐������܂�)���Ƃɒ��ӂ��Ă��������B���ӂ�2�悵�āA 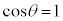 (
(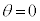 )�́A
)�́A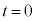 �̏�ԂȂ̂ŁA
�̏�ԂȂ̂ŁA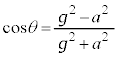 �@����D
�@����D
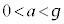 �Ƃ����������t���Ă���̂ŁA
�Ƃ����������t���Ă���̂ŁA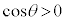 �ł��B
�ł��B
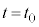 �ɂ����鏬���̍����́A�����͍���h�̍ʼn��_����
�ɂ����鏬���̍����́A�����͍���h�̍ʼn��_����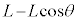 ���������ʒu�ɂ���̂ŁA
���������ʒu�ɂ���̂ŁA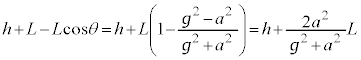 �c�c[��]
�c�c[��]
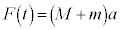 �@����E
�@����E�Ƃ���̂͌��ł��B��́A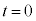 ����
����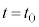 �܂ł�
�܂ł�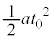 �i�ނ̂ł����A������
�i�ނ̂ł����A������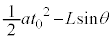 �����i�݂܂���B��蕶���A��̉����x��a�ł����A�����̉����x��a�����������̂ł��B
�����i�݂܂���B��蕶���A��̉����x��a�ł����A�����̉����x��a�����������̂ł��B
���̒��͂�T�Ƃ��āA��̉^���������́A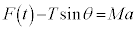
�ł����A������x�����̉����x��b�Ƃ��āA������x�����̉^���������́A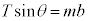
�ł��B������ӁX�����Ă��A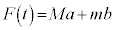 (
(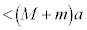 )�ƂȂ�E�ɂȂ�܂���B���̈Ӗ��Ŗ�蕶�͗͂�
)�ƂȂ�E�ɂȂ�܂���B���̈Ӗ��Ŗ�蕶�͗͂�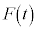 �Ə����Ă��āA
�Ə����Ă��āA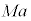 �͈��ł����A��
�͈��ł����A��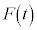 �͈��ł͂���܂���B
�͈��ł͂���܂���B
��L�ł́A���Ŋ����͂̂����d�����l���ĉ��܂������A����ŗ͊w�I�G�l���M�[�ۑ����l���悤�Ƃ���ƁA�����̑��x�̐ڐ�����������v�Ƃ��āA�����̐ڐ������̉^���������́A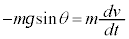 �C�@�������̉^����������
�C�@�������̉^����������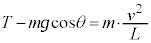
�ƂȂ�̂ł����A����̉�������t �̊��Ƃ��āA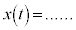 �C
�C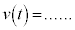 �C
�C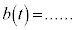 �Ƃ����`�ɂ��܂��\���Ȃ����Ƃ��m���Ă��܂��B��̑��x
�Ƃ����`�ɂ��܂��\���Ȃ����Ƃ��m���Ă��܂��B��̑��x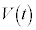 ����
����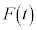 ��t �̊��Ƃ��Ă��܂��\���܂���B(3)��
��t �̊��Ƃ��Ă��܂��\���܂���B(3)��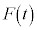 �̃O���t��I����̂����̂��߂ł��B��
�̃O���t��I����̂����̂��߂ł��B��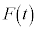 �̂����d��W���A
�̂����d��W���A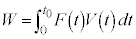 �Ƃ����`�Ōv�Z���邱�Ƃ��ł��Ȃ��̂ŁA����ŗ͊w�I�G�l���M�[�ۑ����l���ĉ��邱�Ƃ��ł��܂���B�����ŁA��L�ł́A���Ō��āA
�Ƃ����`�Ōv�Z���邱�Ƃ��ł��Ȃ��̂ŁA����ŗ͊w�I�G�l���M�[�ۑ����l���ĉ��邱�Ƃ��ł��܂���B�����ŁA��L�ł́A���Ō��āA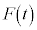 ���o�Ă��Ȃ��`�ŗ͊w�I�G�l���M�[�ۑ����l���ĉ��܂����B��L�̂悤�ɁA�����x�^�����镨�̏�(���n)�ɂ����Ă��A�����͂̂���d�����܂߂ė͊w�I�G�l���M�[�ۑ����l���邱�Ƃ��ł��܂��B�ȉ��̃����N��ŁA�������̗�Œ��ׂĂ݂܂��B���n�ɂ�����G�l���M�[�ۑ����Q�Ƃ��Ă��������B
���o�Ă��Ȃ��`�ŗ͊w�I�G�l���M�[�ۑ����l���ĉ��܂����B��L�̂悤�ɁA�����x�^�����镨�̏�(���n)�ɂ����Ă��A�����͂̂���d�����܂߂ė͊w�I�G�l���M�[�ۑ����l���邱�Ƃ��ł��܂��B�ȉ��̃����N��ŁA�������̗�Œ��ׂĂ݂܂��B���n�ɂ�����G�l���M�[�ۑ����Q�Ƃ��Ă��������B
(2) 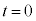 �ɂ����鏬���̈ʒu�������̈ʒu�G�l���M�[�̊�Ƃ���A
�ɂ����鏬���̈ʒu�������̈ʒu�G�l���M�[�̊�Ƃ���A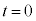 �ɂ����ď����猩���͊w�I�G�l���M�[��0�ł��B
�ɂ����ď����猩���͊w�I�G�l���M�[��0�ł��B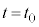 �ɂ����ď����猩����Ə����̑��x��
�ɂ����ď����猩����Ə����̑��x��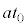 �ň�v���܂��B
�ň�v���܂��B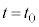 �ɂ����鏬���̈ʒu�G�l���M�[�́A(1)�̌��ʂ��A
�ɂ����鏬���̈ʒu�G�l���M�[�́A(1)�̌��ʂ��A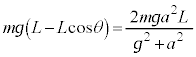 �Ȃ̂ŁA
�Ȃ̂ŁA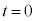 ��
��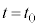 �Ƃ̊Ԃ̗͊w�I�G�l���M�[�ۑ����A��
�Ƃ̊Ԃ̗͊w�I�G�l���M�[�ۑ����A��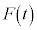 �������d��W�́A
�������d��W�́A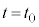 �ɂ������ƕ��̂̉^���G�l���M�[�A���̂̈ʒu�G�l���M�[�̘a�ɓ������A
�ɂ������ƕ��̂̉^���G�l���M�[�A���̂̈ʒu�G�l���M�[�̘a�ɓ������A 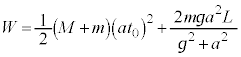 ......[��]
......[��]
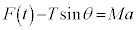 �@����F
�@����F�ł����A������x�����̉����x��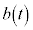 �Ƃ��āA������x�����̉^���������́A
�Ƃ��āA������x�����̉^���������́A 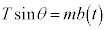 �@����G
�@����G�F�{�G���A
���Ō��āA�����̑�����v�Ƃ��āA�����̎��̕����̉^���������́A
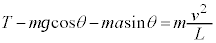 �@����H
�@����H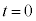 �ɂ����āA
�ɂ����āA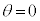 �Ȃ̂ŇG���
�Ȃ̂ŇG���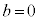 �ł���A
�ł���A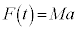 �ł��B����āA�A�C�C�C�E�̂ǂꂩ�ł��B����
�ł��B����āA�A�C�C�C�E�̂ǂꂩ�ł��B����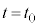 �ŁA�����̍������͂��߂čő�ƂȂ����Ƃ��A�D���
�ŁA�����̍������͂��߂čő�ƂȂ����Ƃ��A�D���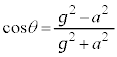 �ł����A
�ł����A
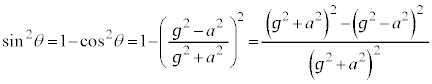
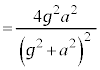
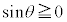 ���A
���A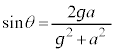
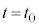 �ɂ����āA���Ō���
�ɂ����āA���Ō���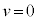 �ƂȂ�̂ŁA�H���A
�ƂȂ�̂ŁA�H���A
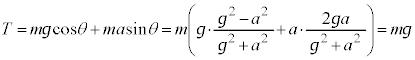
���̂Ƃ��A�G���A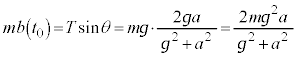
 �@(��
�@(�� 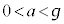 )����āA
)����āA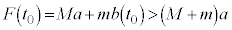
�����Ȃ��Ă���O���t�́A�C ......[��]
(4) �T(3)�̒��D�ŏ������悤�ɁA�_Q�͎��̗��[�Ɏ���M�Cm�̕��̂��ʒu����Ƃ����Ƃ��̏d�S�ł��B����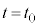 �ɂ����āA(2)�ŏ������悤�ɁA������������x��
�ɂ����āA(2)�ŏ������悤�ɁA������������x��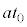 �Ȃ̂ŁAQ�̑��x��x������u�Ƃ��ďd�SQ�Ɏ���
�Ȃ̂ŁAQ�̑��x��x������u�Ƃ��ďd�SQ�Ɏ���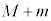 ������ƍl���A�^���ʕۑ����A
������ƍl���A�^���ʕۑ����A 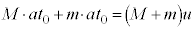 �@��
�@�� 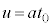 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��] ......[��]
......[��] ......[��]
......[��]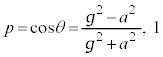
 �@����D
�@����D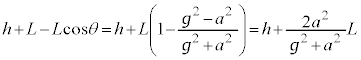 �c�c[��]
�c�c[��]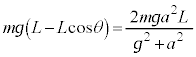 �Ȃ̂ŁA
�Ȃ̂ŁA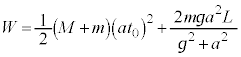 ......[��]
......[��]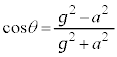 �ł����A
�ł����A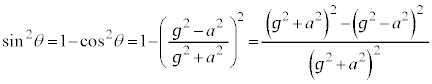
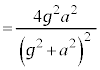
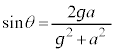
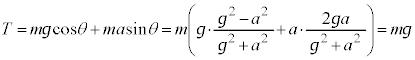
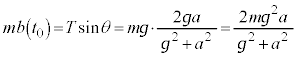
 �@(��
�@(�� 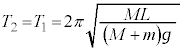 ......[��]
......[��]