��嗝�n���w'25�N�O��[2]
p��m�������Ƃ��A��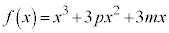 ��
��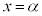 �ŋɑ�l���Ƃ�A
�ŋɑ�l���Ƃ�A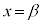 �ŋɏ��l���Ƃ�Ƃ���B
�ŋɏ��l���Ƃ�Ƃ���B
(1) 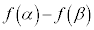 ��p��m��p���ĕ\���B
��p��m��p���ĕ\���B (2) p��m��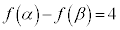 �����Ȃ��瓮���Ƃ��A�Ȑ�
�����Ȃ��瓮���Ƃ��A�Ȑ�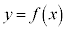 �̕ϋȓ_�̋O�Ղ����߂�B
�̕ϋȓ_�̋O�Ղ����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��吔�w�ł͕p�o�^�C�v�̖��ł��B
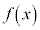 ��
��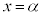 �ŋɑ�l���Ƃ�A
�ŋɑ�l���Ƃ�A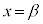 �ŋɏ��l���Ƃ�(���̑������Q�ƁB�܂��A
�ŋɏ��l���Ƃ�(���̑������Q�ƁB�܂��A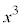 �̌W����1�Ȃ̂ŁA
�̌W����1�Ȃ̂ŁA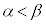 �ł�)���Ƃ���A
�ł�)���Ƃ���A
����āA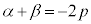 �C
�C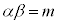 �@����@
�@����@
�ł��B
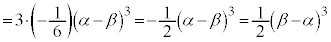 �@(��
�@(�� 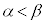 )
)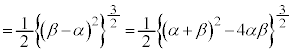 �@(��{�Ώ̎����Q��)
�@(��{�Ώ̎����Q��)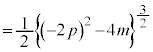 �@(�� �@)
�@(�� �@)
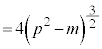 ......[��]
......[��]
(2) (1)���A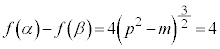
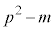 �͎����Ȃ̂�
�͎����Ȃ̂�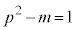 �@����A3����
�@����A3����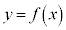 �̃O���t�͕ϋȓ_�Ɋւ��đΏ�(3�����̃O���t���Q��)�ŁA�ϋȓ_�́A�ɑ�_
�̃O���t�͕ϋȓ_�Ɋւ��đΏ�(3�����̃O���t���Q��)�ŁA�ϋȓ_�́A�ɑ�_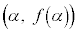 �Ƌɏ��_
�Ƌɏ��_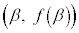 �̒��_�ł��B����āA�ϋȓ_�̍��W
�̒��_�ł��B����āA�ϋȓ_�̍��W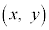 ��
��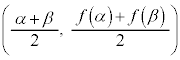 �ŗ^�����܂��B�@���A�ϋȓ_��x���W�́A
�ŗ^�����܂��B�@���A�ϋȓ_��x���W�́A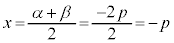 �@����B
�@����B2����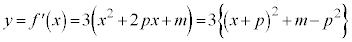 �̃O���t�̎���
�̃O���t�̎���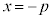 �ł��B
�ł��B
�ϋȓ_��y���W�ɂ��āA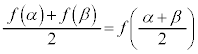 �ƂȂ�܂����A������m���߂Ă����܂��B2�����̃O���t�͎�
�ƂȂ�܂����A������m���߂Ă����܂��B2�����̃O���t�͎�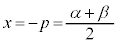 �Ɋւ��đΏ̂Ȃ̂ŁA
�Ɋւ��đΏ̂Ȃ̂ŁA �� 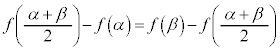 ����āA
����āA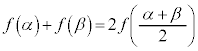 �ł��B
�ł��B
�]���āA�@���A�ϋȓ_��y���W�́A 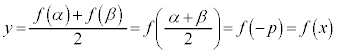 �@(�� �B)
�@(�� �B)�A�C�B���A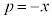 �C
�C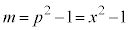 �C����āA
�C����āA 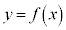 ���O���́A
���O���́A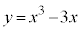 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 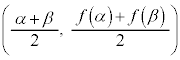 �ŗ^�����܂��B�@���A�ϋȓ_��x���W�́A
�ŗ^�����܂��B�@���A�ϋȓ_��x���W�́A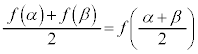 �ƂȂ�܂����A������m���߂Ă����܂��B
�ƂȂ�܂����A������m���߂Ă����܂��B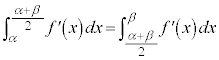
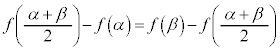
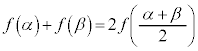 �ł��B
�ł��B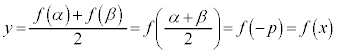 �@(�� �B)
�@(�� �B)