��嗝�n���w'25�N�O��[3]
���W��Ԃ�3�_O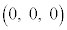 �CA
�CA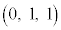 �CP
�CP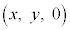 ������B
������B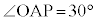 ����
����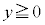 �����悤�ɓ_P�������Ƃ��A
�����悤�ɓ_P�������Ƃ��A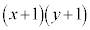 �̍ő�l�ƍŏ��l�����߂�B
�̍ő�l�ƍŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���������̂������ł͂Ȃ��Ȑ�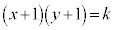 �ł����A���`�v��@�̉��p���ł��B
�ł����A���`�v��@�̉��p���ł��B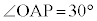 �ƂȂ�悤��P�����Ɖ~���ʂ�`���܂����A���̖��ł�P��z���W��0�Ȃ̂ŁAP�͉~���ʂ�xy���ʂŐ�������ɂł���ȉ~������ƂɂȂ�܂�(2���Ȑ��̕������Q��)�B
�ƂȂ�悤��P�����Ɖ~���ʂ�`���܂����A���̖��ł�P��z���W��0�Ȃ̂ŁAP�͉~���ʂ�xy���ʂŐ�������ɂł���ȉ~������ƂɂȂ�܂�(2���Ȑ��̕������Q��)�B
����āA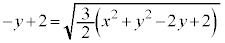
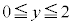 �̂��ƂɁA
�̂��ƂɁA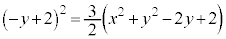
������ȉ~�ł��B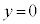 �̂Ƃ�
�̂Ƃ�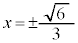 �C
�C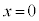 �̂Ƃ�
�̂Ƃ�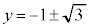 (
(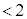 )�Ȃ̂ŁA
)�Ȃ̂ŁA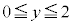 ���AP�̑��ݔ͈͂́A�ȉ~�@��
���AP�̑��ݔ͈͂́A�ȉ~�@��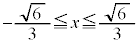 �̕����ł��B
�̕����ł��B
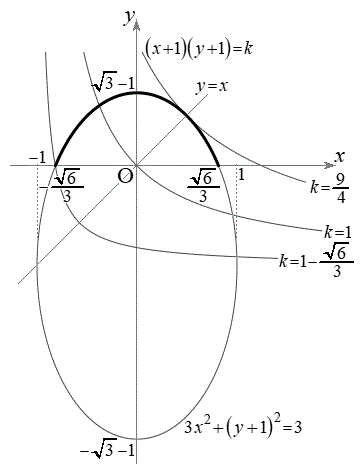 k��萔�Ƃ��āA
k��萔�Ƃ��āA
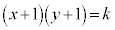 �@����A
�@����A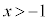 �͈̔͂ł͉��ɓʂȒ��p�o�Ȑ��ŁA���̃O���t�͒���
�͈̔͂ł͉��ɓʂȒ��p�o�Ȑ��ŁA���̃O���t�͒���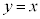 �Ɋւ��đΏ̂ł��Bk��傫������ƁA�A�̃O���t�͉E��ɂ���܂��B
�Ɋւ��đΏ̂ł��Bk��傫������ƁA�A�̃O���t�͉E��ɂ���܂��B
k��ω������āA�@�ƇA�̃O���t��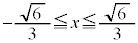 �͈̔͂ɋ��L�_�����������l���܂��B
�͈̔͂ɋ��L�_�����������l���܂��B
k���ŏ��ɂȂ�Ƃ��A�A�̃O���t��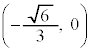 ��ʂ�܂��B���̂Ƃ��A
��ʂ�܂��B���̂Ƃ��A
�ł��B
k���ő�ɂȂ�Ƃ��A�@�ƇA�̃O���t����1�ی��Őڂ��܂��B��L�̂悤�ɁA���p�o�Ȑ��A�́A����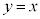 �Ɋւ��đΏ̂Ȃ̂ŁA�@�ƇA�̐ړ_������
�Ɋւ��đΏ̂Ȃ̂ŁA�@�ƇA�̐ړ_������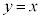 ��ɑ��݂��܂��B�@��
��ɑ��݂��܂��B�@��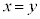 �Ƃ���ƁA
�Ƃ���ƁA
���̂Ƃ��A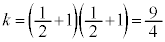
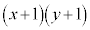 �̍ő�l��
�̍ő�l��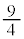 �C�ŏ��l��
�C�ŏ��l��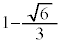 ......[��]
......[��]
�ʉ��D�W���I�ȉ�@�ʼn����Ă݂܂��B�A���A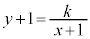 ���@�ɑ������ƁA
���@�ɑ������ƁA 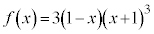 �Ƃ����܂��B
�Ƃ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 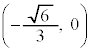 ��ʂ�܂��B���̂Ƃ��A
��ʂ�܂��B���̂Ƃ��A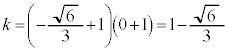
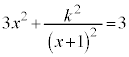
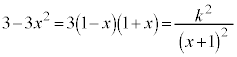
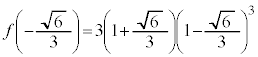
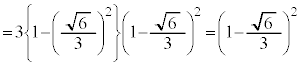
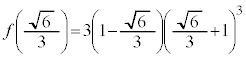
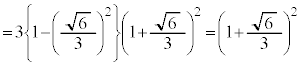
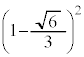
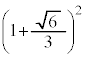
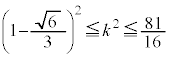 �̂Ƃ�(�����@�̕������ւ̉��p(2)���Q��)�B�Ȃ��A
�̂Ƃ�(�����@�̕������ւ̉��p(2)���Q��)�B�Ȃ��A