大阪大学2025年物理入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 水平な床の上を運動する台と、台の上にのせた小物体について考察する。台および小物体はx軸に沿ってのみ運動するものとする。重力加速度の大きさは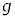 である。加速度の正の向きはx軸の正の向きとする。
である。加速度の正の向きはx軸の正の向きとする。
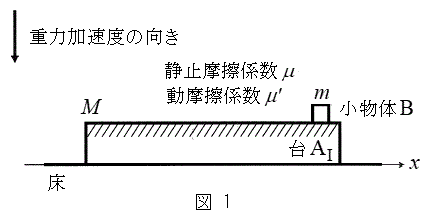 Ⅰ.図1のように、水平な床の上に質量Mの台
Ⅰ.図1のように、水平な床の上に質量Mの台 を静止させ、台
を静止させ、台 の上に質量mの小物体Bを静止させた。台
の上に質量mの小物体Bを静止させた。台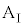 と小物体Bの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は
と小物体Bの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は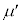 (ただし
(ただし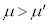 )である。床と台
)である。床と台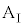 の間には摩擦はないものとする。また、小物体Bをのせた台
の間には摩擦はないものとする。また、小物体Bをのせた台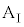 の面は水平である。なお、台
の面は水平である。なお、台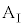 の長さは十分に長く、小物体Bは台
の長さは十分に長く、小物体Bは台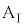 の上から滑り落ちないものとする。
の上から滑り落ちないものとする。時刻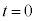 から、台
から、台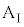 に対してx軸の正の向きに大きさが
に対してx軸の正の向きに大きさが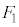 の一定の力を加え続けた。
の一定の力を加え続けた。
問1 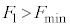 のとき、小物体Bは台
のとき、小物体Bは台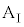 に対してすべるように運動した。また、
に対してすべるように運動した。また、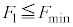 のとき、台
のとき、台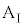 と小物体Bは一体となって運動した。
と小物体Bは一体となって運動した。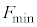 を、
を、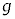 ,M,m,μ,
,M,m,μ,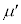 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問2 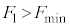 のとき、時刻
のとき、時刻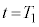 (
(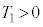 )における、台
)における、台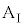 の速度
の速度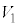 と小物体Bの速度
と小物体Bの速度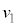 を、
を、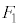 ,
,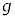 ,M,m,
,M,m,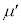 ,
,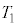 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。
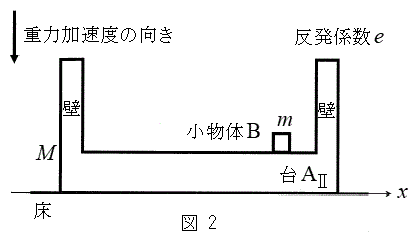 Ⅱ.図2のように、両端に壁をもつ質量Mの台
Ⅱ.図2のように、両端に壁をもつ質量Mの台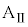 を水平な床の上に静止させ、台
を水平な床の上に静止させ、台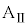 の上に質量mの小物体Bを静止させた。台
の上に質量mの小物体Bを静止させた。台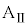 の壁と小物体Bとの間の反発係数(はねかえり係数)をeとし、
の壁と小物体Bとの間の反発係数(はねかえり係数)をeとし、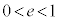 が満たされているとする。台
が満たされているとする。台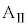 と小物体Bの間、および、床と台
と小物体Bの間、および、床と台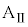 の間に摩擦はないものとする。また、小物体Bをのせた台
の間に摩擦はないものとする。また、小物体Bをのせた台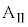 の面は水平である。
の面は水平である。時刻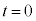 から時刻
から時刻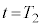 (
(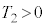 )までの間、台
)までの間、台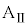 に対してx軸の正の向きに大きさが
に対してx軸の正の向きに大きさが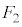 の一定の力を加え続けた。時刻
の一定の力を加え続けた。時刻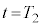 での、台
での、台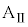 と小物体Bの速度はそれぞれ
と小物体Bの速度はそれぞれ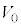 と
と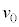 であった。なお、この間に、小物体Bは台
であった。なお、この間に、小物体Bは台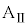 の壁に衝突することはなかった。
の壁に衝突することはなかった。
問3 小物体Bの速度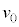 および時刻
および時刻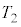 を、
を、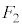 ,M,m,
,M,m,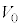 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。 時刻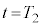 において、台
において、台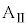 に対して力を加えることをやめた。その後、小物体Bは台
に対して力を加えることをやめた。その後、小物体Bは台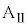 の壁と衝突を繰り返した。
の壁と衝突を繰り返した。
問4 十分に長い時間、衝突を繰り返した結果、台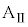 と小物体Bの速度はどちらも
と小物体Bの速度はどちらも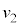 となった。速度
となった。速度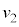 を、e,
を、e,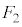 ,M,m,
,M,m,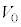 のうち必要なものを用いてそれぞれ表せ。
のうち必要なものを用いてそれぞれ表せ。
問5 小物体Bと壁がn回目の衝突をした直後の、台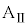 の速度
の速度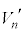 および小物体Bの速度
および小物体Bの速度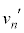 を、e,
を、e,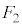 ,M,m,n,
,M,m,n,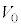 のうち必要なものを用いてそれぞれ表せ。ただし、nは1以上の整数とする。
のうち必要なものを用いてそれぞれ表せ。ただし、nは1以上の整数とする。
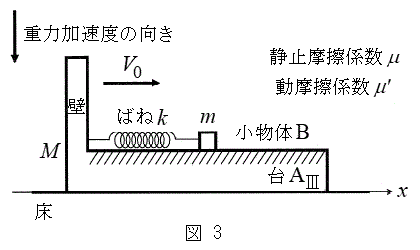 Ⅲ.図3のように、水平な床の上に質量Mの台
Ⅲ.図3のように、水平な床の上に質量Mの台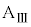 を静止させ、台
を静止させ、台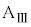 の上に質量mの小物体Bを静止させた。さらに、台
の上に質量mの小物体Bを静止させた。さらに、台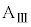 の壁と小物体Bを、質量の無視できるばね定数kのばねでつないだ。台
の壁と小物体Bを、質量の無視できるばね定数kのばねでつないだ。台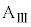 と小物体Bとの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は
と小物体Bとの間には摩擦があり、その静止摩擦係数はμ,動摩擦係数は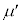 (ただし、
(ただし、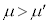 )とする。床と台
)とする。床と台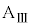 の間には摩擦はないものとする。また、小物体Bをのせた台
の間には摩擦はないものとする。また、小物体Bをのせた台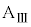 の面は水平である。
の面は水平である。最初、ばねの長さは自然長dであった。台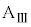 に対して、x軸の正の向きに瞬間的な力を加えたところ、その直後の台
に対して、x軸の正の向きに瞬間的な力を加えたところ、その直後の台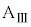 の速度は
の速度は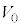 となり、小物体Bは台
となり、小物体Bは台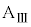 の上をすべりはじめた。しばらくの間、ばねは伸び縮みを繰り返し、その後、ばねの長さはLとなり変化しなくなった。また、このときの台
の上をすべりはじめた。しばらくの間、ばねは伸び縮みを繰り返し、その後、ばねの長さはLとなり変化しなくなった。また、このときの台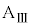 と小物体Bの速度はともに
と小物体Bの速度はともに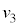 であった。なお、この運動の間、小物体Bは台
であった。なお、この運動の間、小物体Bは台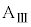 の壁に衝突したり、台
の壁に衝突したり、台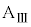 の上からすべり落ちることはなかった。
の上からすべり落ちることはなかった。
問6 速度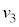 を、d,
を、d,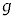 ,k,M,m,
,k,M,m,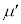 ,
,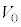 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問7 小物体Bが台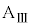 の上をすべり始めてからばねの長さが変化しなくなるまでの間に、小物体Bが台
の上をすべり始めてからばねの長さが変化しなくなるまでの間に、小物体Bが台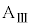 の上をすべった総距離をd,
の上をすべった総距離をd,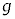 ,k,L,M,m,
,k,L,M,m,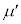 ,
,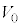 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。 台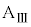 が速度
が速度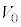 を得てから、ばねの長さがLとなり変化しなくなるまでの間の、小物体Bの運動について考察する。小物体Bが台
を得てから、ばねの長さがLとなり変化しなくなるまでの間の、小物体Bの運動について考察する。小物体Bが台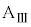 の上をすべりはじめると、ばねは縮みはじめた。ばねの長さが
の上をすべりはじめると、ばねは縮みはじめた。ばねの長さが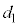 となったとき、小物体Bは台
となったとき、小物体Bは台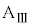 の上で1回目の折り返しを行い、ばねは伸び始めた。その後、ばねの長さが
の上で1回目の折り返しを行い、ばねは伸び始めた。その後、ばねの長さが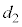 となったとき、小物体Bは台
となったとき、小物体Bは台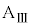 の上で2回目の折り返しを行い、ばねは再び縮みはじめた。以後、ばねはこのような伸び縮みを繰り返した。小物体Bは台
の上で2回目の折り返しを行い、ばねは再び縮みはじめた。以後、ばねはこのような伸び縮みを繰り返した。小物体Bは台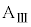 の上でn回目の折り返しを行ったのち、
の上でn回目の折り返しを行ったのち、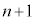 回目の折り返しをすることなく、台
回目の折り返しをすることなく、台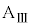 に対する運動を停止した。そしてそれ以降、ばねの長さは変化しなくなった。ここで、nは3以上の整数とする。
に対する運動を停止した。そしてそれ以降、ばねの長さは変化しなくなった。ここで、nは3以上の整数とする。
問8 台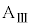 が速度
が速度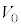 を得てから小物体Bが1回目の折り返しをするまでの間の運動を考える。その間のある時刻において、ばねの長さはDであった。その時刻における、台
を得てから小物体Bが1回目の折り返しをするまでの間の運動を考える。その間のある時刻において、ばねの長さはDであった。その時刻における、台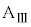 とともに運動する観測者からみた小物体Bの加速度aを、D,d,
とともに運動する観測者からみた小物体Bの加速度aを、D,d,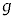 ,k,M,m,
,k,M,m,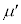 ,
,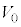 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
問9 1回目の折り返しの時点でのばねの長さ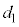 を、d,
を、d,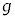 ,k,M,m,
,k,M,m,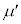 ,
,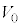 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。 問10 小物体Bが台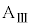 に対して運動を停止した後のばねの長さLを、d,
に対して運動を停止した後のばねの長さLを、d,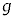 ,k,M,m,
,k,M,m,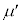 ,n,
,n,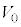 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
[解答へ]
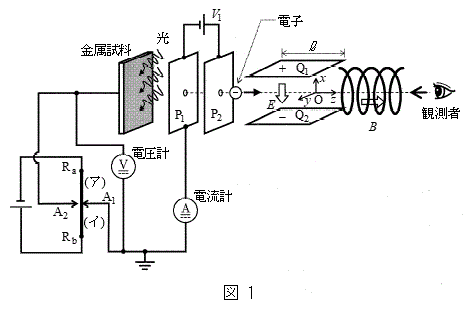 [2] ある振動数νと強さIをもつ光を金属試料に照射し、光電効果により発生する光電子の運動について考察する。図1のように、真空中に装置を置き、原点をOとする直交座標系x,y,zを設定する。まず、微小な穴をもつ電極
[2] ある振動数νと強さIをもつ光を金属試料に照射し、光電効果により発生する光電子の運動について考察する。図1のように、真空中に装置を置き、原点をOとする直交座標系x,y,zを設定する。まず、微小な穴をもつ電極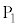 と金属試料をz軸に直交するように配置し、電極
と金属試料をz軸に直交するように配置し、電極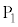 に対して金属材料に電圧Vを与える回路を設ける。この回路には、一様な抵抗線
に対して金属材料に電圧Vを与える回路を設ける。この回路には、一様な抵抗線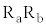 の間に端子
の間に端子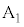 ,および
,および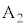 が接続されている。端子
が接続されている。端子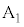 の位置は固定されており、端子
の位置は固定されており、端子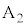 の接続位置を変えることにより、電圧Vを設定したい値に調整することができる。
の接続位置を変えることにより、電圧Vを設定したい値に調整することができる。
次に、微小な穴をもつ電極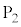 をz軸に直交するように配置し、電極
をz軸に直交するように配置し、電極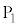 に対して電圧
に対して電圧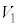 (
(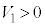 )を加える。電極
)を加える。電極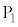 と
と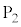 に設けられた微小な穴の中心は、z軸上に配置されている。z軸方向の長さが
に設けられた微小な穴の中心は、z軸上に配置されている。z軸方向の長さが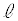 で、2枚の平行な電極
で、2枚の平行な電極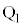 と
と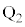 の間には、強さEの一様な電場(電界)がx軸の負の向きにかかっている。ソレノイド内にはz軸の正の向きに一様な磁場(磁界)があり、その磁束密度の大きさはBである。観測者は、z軸上において、z軸の負の向きを向いている。また、電子がもつ電気量と質量をそれぞれ
の間には、強さEの一様な電場(電界)がx軸の負の向きにかかっている。ソレノイド内にはz軸の正の向きに一様な磁場(磁界)があり、その磁束密度の大きさはBである。観測者は、z軸上において、z軸の負の向きを向いている。また、電子がもつ電気量と質量をそれぞれ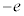 (eは電気素量)とm,プランク定数をhとする。
(eは電気素量)とm,プランク定数をhとする。
ただし、以下の問では、金属試料に照射する光の振動数νまたは強さIのいずれかを変更する場合、他方は変わらないものとする。金属試料と電極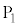 の間、電極
の間、電極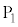 と
と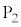 の間、および、電極
の間、および、電極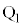 と
と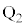 の間以外の場所には電場は無いものとする。また、電極
の間以外の場所には電場は無いものとする。また、電極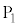 と
と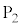 の材質は常に金属試料と同じものを用いる。さらに、電極
の材質は常に金属試料と同じものを用いる。さらに、電極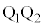 間を通過した電子は、その瞬間にソレノイドに入るものとする。電極
間を通過した電子は、その瞬間にソレノイドに入るものとする。電極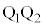 間の間隔、および、ソレノイドの直径は十分に大きく、進行中の電子がこれらに衝突することはない。簡単のため、ソレノイド外部の磁場は無視でき、また、ソレノイドは十分に長いものとする。なお、光電子は質点として扱い、量子的な波動性は無視でき、その運動は重力の影響を受けないものとする。
間の間隔、および、ソレノイドの直径は十分に大きく、進行中の電子がこれらに衝突することはない。簡単のため、ソレノイド外部の磁場は無視でき、また、ソレノイドは十分に長いものとする。なお、光電子は質点として扱い、量子的な波動性は無視でき、その運動は重力の影響を受けないものとする。
Ⅰ.仕事関数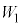 をもつ金属試料(金属試料1とする)に光を照射した。端子
をもつ金属試料(金属試料1とする)に光を照射した。端子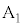 と
と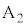 の接続位置が一致する場合には、試料表面から光電子が飛び出した。次に端子
の接続位置が一致する場合には、試料表面から光電子が飛び出した。次に端子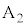 の位置を変え、電圧Vを徐々に大きくすると、電極
の位置を変え、電圧Vを徐々に大きくすると、電極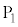 に到達する光電子の数は減少し、
に到達する光電子の数は減少し、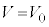 においてその数は0になった。
においてその数は0になった。
問1 このとき、端子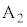 の接続位置は、図1における(ア)
の接続位置は、図1における(ア)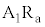 間、もしくは(イ)
間、もしくは(イ)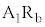 間のどちらの範囲内で調整したか、(ア)または(イ)の記号で答えよ。
間のどちらの範囲内で調整したか、(ア)または(イ)の記号で答えよ。
問2 仕事関数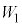 をν,e,h,
をν,e,h,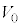 を用いて表せ。
を用いて表せ。
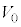 よりもわずかに小さい電圧Vにおいて、電極
よりもわずかに小さい電圧Vにおいて、電極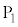 に到達した電子の一部が穴を通過した。そして、電極
に到達した電子の一部が穴を通過した。そして、電極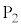 の穴も通り抜けて、z軸の正の向きに進んだ。ただし、電極
の穴も通り抜けて、z軸の正の向きに進んだ。ただし、電極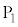 での電子の初速度は無視できるものとする。
での電子の初速度は無視できるものとする。
問3 電極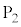 の穴を通過した瞬間の電子の速さ
の穴を通過した瞬間の電子の速さ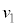 をe,m,
をe,m,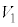 を用いて表せ。
を用いて表せ。
問4 問3の電子が電極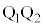 間を通過し、ソレノイドに入った瞬間の速度のx成分
間を通過し、ソレノイドに入った瞬間の速度のx成分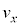 を、e,
を、e,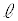 ,m,
,m,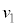 ,Eを用いて表せ。
,Eを用いて表せ。
問5 z軸上の観測者からは、ソレノイド内を進行する電子が等速円運動しているように見える。この円運動の角速度をe,m,Bを用いて表せ。
Ⅱ.次に、金属試料1を金属試料2に交換した。金属試料2の仕事関数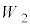 は
は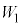 よりもw(
よりもw(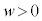 )だけ小さく、
)だけ小さく、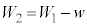 の関係がある。電極
の関係がある。電極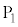 と金属試料2の間の電圧が
と金属試料2の間の電圧が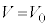 になるように、端子
になるように、端子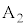 の接続位置を調整し、金属試料2に光を照射して光電子を発生させた。このとき、z軸の正の向きに進行し、電極
の接続位置を調整し、金属試料2に光を照射して光電子を発生させた。このとき、z軸の正の向きに進行し、電極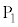 の穴を通過して瞬間の電子の初速度の大きさは、照射する光の強さIによらず、0から
の穴を通過して瞬間の電子の初速度の大きさは、照射する光の強さIによらず、0から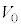 の範囲内で連続的に分布した。
の範囲内で連続的に分布した。
問6 電極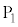 の穴を通過する電子がもちうる最大の初速度の大きさ
の穴を通過する電子がもちうる最大の初速度の大きさ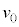 をm,wを用いて表せ。
をm,wを用いて表せ。
以下では、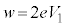 となる金属試料2を用いる場合を考える。
となる金属試料2を用いる場合を考える。
問7 問6で求めた最大の初速度の大きさ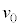 をもつ電子が電極
をもつ電子が電極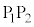 間と電極
間と電極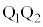 間を通過し、ソレノイド内を進行した。z軸上の観測者がこの電子を持た場合の等速円運動の半径は、問5における等速円運動の半径の何倍になるか、答えよ。
間を通過し、ソレノイド内を進行した。z軸上の観測者がこの電子を持た場合の等速円運動の半径は、問5における等速円運動の半径の何倍になるか、答えよ。
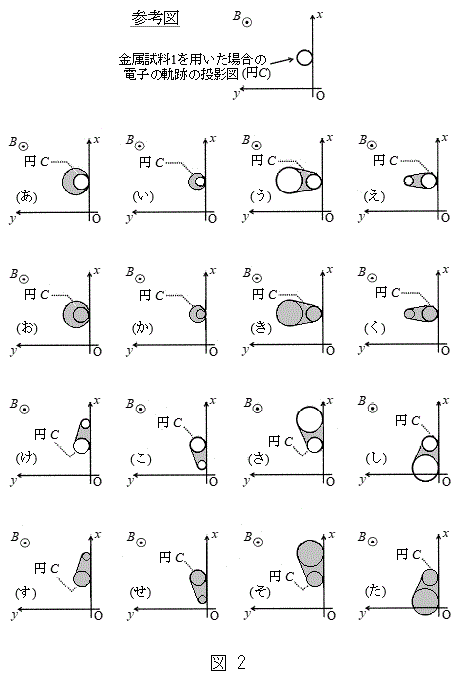 問8 十分に長い時間、金属試料2に光を照射した。その間に発生し、z軸の正向きに進行するすべての電子について考える。ソレノイド内を進行する電子の軌跡をxy平面上に投影した図(投影図)は、観測者にどのように見えるか。図2の(あ)~(た)の中から最も適切なものを選んで記号で答えよ。ただし、(あ)~(た)では電子の軌跡が投影される場所を黒色または灰色で表示している。また、(あ)~(た)における円Cは、金属試料1を用いた場合の投影図(図2中の参考図)を表すものとする。
問8 十分に長い時間、金属試料2に光を照射した。その間に発生し、z軸の正向きに進行するすべての電子について考える。ソレノイド内を進行する電子の軌跡をxy平面上に投影した図(投影図)は、観測者にどのように見えるか。図2の(あ)~(た)の中から最も適切なものを選んで記号で答えよ。ただし、(あ)~(た)では電子の軌跡が投影される場所を黒色または灰色で表示している。また、(あ)~(た)における円Cは、金属試料1を用いた場合の投影図(図2中の参考図)を表すものとする。
問9 問8の状況において、ソレノイド内を進行するある1つの電子について考える。その電子のxy平面上の投影図における円の中心座標を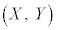 とする。座標X,座標Yの間には、観測するすべての電子において同じ関係式が成り立つ。座標Yをe,
とする。座標X,座標Yの間には、観測するすべての電子において同じ関係式が成り立つ。座標Yをe,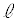 ,m,B,E,Xのうち必要なものを用いて表せ。
,m,B,E,Xのうち必要なものを用いて表せ。
問10 問8の状況において、以下の(ち)~(ぬ)の中のいずれか1つの操作を行ったところ、金属試料1を用いた場合の円Cのみの投影図(図2中の参考図)と同じ投影図が得られた。これが可能となる操作を(ち)~(ぬ)の中からすべて選んで記号で答えよ。
(ち) ν(照射する光の振動数)を変更する操作
(つ) I (照射する光の強さ)うぃ変更する操作
(て) 端子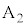 の接続位置を変更する操作
の接続位置を変更する操作 (と) 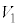 (電極
(電極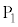 に対する
に対する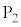 の電圧)を
の電圧)を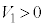 の範囲で変更する操作
の範囲で変更する操作 (な) E(電極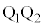 間の電場の強さ)を変更する操作
間の電場の強さ)を変更する操作 (ぬ) B(ソレノイド内の磁束密度の大きさ)を変更する操作
[解答へ]
[3] 以下のAとBの両方の問題に解答せよ。なおAとBは独立した内容の問題である。
A.屈折率(絶対屈折率)が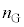 (
(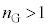 )で一定と見なせる2枚のガラス平板の間に薄膜をはさみ、光の干渉を観察することを考える。ただし、ガラス平板は力を加えても変形せず、厚さも屈折率も変化しないものとする。ガラス平板の厚さは一定で十分に厚いとみなしてよく、上側ガラス平板の上面と下側ガラス平板の下面からの反射光の影響、ガラス平板にかかる重力の影響は無視できるものとする。また、薄膜の厚みは常に一様であり、空気の屈折率は1とする。以下では、すべての屈折率は光の波長に依存しないものとする。
)で一定と見なせる2枚のガラス平板の間に薄膜をはさみ、光の干渉を観察することを考える。ただし、ガラス平板は力を加えても変形せず、厚さも屈折率も変化しないものとする。ガラス平板の厚さは一定で十分に厚いとみなしてよく、上側ガラス平板の上面と下側ガラス平板の下面からの反射光の影響、ガラス平板にかかる重力の影響は無視できるものとする。また、薄膜の厚みは常に一様であり、空気の屈折率は1とする。以下では、すべての屈折率は光の波長に依存しないものとする。
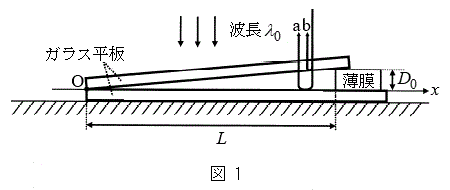 Ⅰ.図1のように、空気中で2枚のガラス平板を重ね、一端に薄膜をはさんだ状態で水平な床の上に置いた。このときの薄膜の厚さは
Ⅰ.図1のように、空気中で2枚のガラス平板を重ね、一端に薄膜をはさんだ状態で水平な床の上に置いた。このときの薄膜の厚さは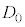 であった。その後、床に対して真上から波長
であった。その後、床に対して真上から波長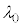 の単色光を当て、真上から観察した。すると、ガラス平板の間にできるくさび形の空気層の下面で反射する光aと空気層の上面で反射する光bが干渉して、明暗のしま模様が観察された。下側ガラス平板の上面に沿ってx軸をとり、上下のガラス平板が接する左端位置を原点Oとする。原点Oから薄膜の左端までの距離Lは、薄膜の厚さに比べて十分に大きいとする。
の単色光を当て、真上から観察した。すると、ガラス平板の間にできるくさび形の空気層の下面で反射する光aと空気層の上面で反射する光bが干渉して、明暗のしま模様が観察された。下側ガラス平板の上面に沿ってx軸をとり、上下のガラス平板が接する左端位置を原点Oとする。原点Oから薄膜の左端までの距離Lは、薄膜の厚さに比べて十分に大きいとする。
問1 位置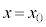 (
(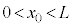 )における、光aとbの経路差の絶対値を、
)における、光aとbの経路差の絶対値を、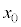 ,
,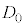 ,Lを用いて表せ。
,Lを用いて表せ。
問2 観察されたしま模様の隣り合う明線の間隔を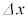 とする。このときの薄膜の厚さ
とする。このときの薄膜の厚さ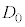 を、
を、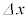 ,L,
,L,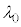 を用いて表せ。
を用いて表せ。 次に、2枚のガラス平板の間にできるくさび形の空間を屈折率n(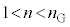 )の媒質で満たした。このとき、薄膜の厚さは
)の媒質で満たした。このとき、薄膜の厚さは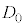 のままであった。この状態で、先ほどと同様に真上から波長
のままであった。この状態で、先ほどと同様に真上から波長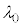 の単色光を当て、光aとbの干渉によるしま模様を観察した。すると、しま模様の明線の間隔
の単色光を当て、光aとbの干渉によるしま模様を観察した。すると、しま模様の明線の間隔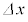 は、問2の状態から変化した。
は、問2の状態から変化した。
さらに、ガラス平板ではさんだ薄膜に力を加えることで、薄膜の厚さが変化する場合を考える。この薄膜は、上から力Fを加えることにより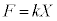 の法則に従って、全体の厚さが一様にXだけ縮むとする。ただし、kは薄膜の特性を表す正の定数である。
の法則に従って、全体の厚さが一様にXだけ縮むとする。ただし、kは薄膜の特性を表す正の定数である。
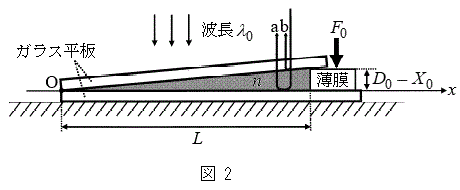 図2のように、2枚のガラス平板の間を屈折率nの媒質で満たしたまま、右端にはさんだ薄膜に力
図2のように、2枚のガラス平板の間を屈折率nの媒質で満たしたまま、右端にはさんだ薄膜に力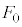 をかけて厚さを
をかけて厚さを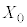 だけ減少させた。この状態で、光aとbの干渉によるしま模様を観測したところ、明線の間隔
だけ減少させた。この状態で、光aとbの干渉によるしま模様を観測したところ、明線の間隔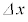 が、問2の場合と同じになった。ただし、屈折率nは変化しない定数であり、上下のガラス平板の接する位置は原点Oから動かず、薄膜と2枚のガラス平板は常に接しているとする。
が、問2の場合と同じになった。ただし、屈折率nは変化しない定数であり、上下のガラス平板の接する位置は原点Oから動かず、薄膜と2枚のガラス平板は常に接しているとする。
問3 このとき、定数kを、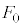 ,
,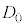 ,nを用いて表せ。
,nを用いて表せ。
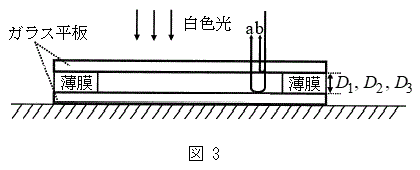 Ⅱ.図3のように、両端に同じ薄膜をはさんだ2枚の平行なガラス平板を水平な床の上に置いた。この状態で、ガラス平板の真上から白色光を当てた。以下では、2枚のガラス平板の間にはさまれた空気層の下面で反射する光aと、空気層の上面で反射する光bの干渉により強め合う光について考える。ガラス平板をのせた状態で、両端の薄膜の厚さは
Ⅱ.図3のように、両端に同じ薄膜をはさんだ2枚の平行なガラス平板を水平な床の上に置いた。この状態で、ガラス平板の真上から白色光を当てた。以下では、2枚のガラス平板の間にはさまれた空気層の下面で反射する光aと、空気層の上面で反射する光bの干渉により強め合う光について考える。ガラス平板をのせた状態で、両端の薄膜の厚さは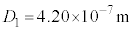 であった。このとき、波長
であった。このとき、波長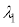 の可視光が干渉により強められた。ただし、可視光の波長範囲を
の可視光が干渉により強められた。ただし、可視光の波長範囲を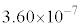 ~
~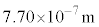 とし、白色光は可視光の波長をすべて含むものとする。
とし、白色光は可視光の波長をすべて含むものとする。
問4 波長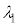 は何mか、有効数字2桁で求めよ。
は何mか、有効数字2桁で求めよ。 この状態から、上側ガラス平板の上面に一様な力を徐々に加え、両端の薄膜の厚さを一様に小さくすることで、2枚のガラス平板を平行に保ちつつ空気層の厚さをゆっくりと変化させた。すると、干渉により強め合う光の波長が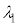 から連続的に変化し、薄膜の厚さが
から連続的に変化し、薄膜の厚さが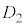 より小さくなったところで強め合う光の波長が可視光の波長範囲から外れた。さらに力を徐々に大きくして厚さを変化させたところ、薄膜の厚さが
より小さくなったところで強め合う光の波長が可視光の波長範囲から外れた。さらに力を徐々に大きくして厚さを変化させたところ、薄膜の厚さが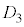 より小さくなったときに、再び強め合う光の波長が可視光の波長範囲に入った。
より小さくなったときに、再び強め合う光の波長が可視光の波長範囲に入った。
問5 厚さ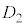 ,
,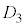 は何mか、それぞれ有効数字2桁で求めよ。
は何mか、それぞれ有効数字2桁で求めよ。
B.重陽子(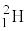 )とベリリウム(
)とベリリウム(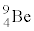 )の核反応
)の核反応
および
を用いて中性子(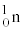 )を発生させることを考える。最初
)を発生させることを考える。最初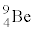 は静止しており、静電気力が無視できるほど十分に遠方から、加速した
は静止しており、静電気力が無視できるほど十分に遠方から、加速した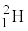 や
や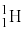 を
を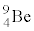 に正面衝突させた。
に正面衝突させた。
 電気素量は
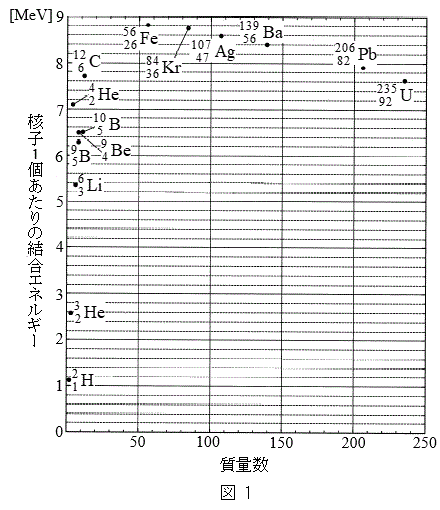
電気素量は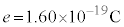 とする。必要ならば、図1に示した核子1個あたりの結合エネルギーと質量数の関係を用いよ。以下では、原子核および中性子はの速さは真空中での光の速さに比べて十分に小さく、核反応は真空中で起こるものとする。原子核および中性子は質点として扱い、量子的な波動性は無視できる。また、重力の影響は無視できるものとする。
とする。必要ならば、図1に示した核子1個あたりの結合エネルギーと質量数の関係を用いよ。以下では、原子核および中性子はの速さは真空中での光の速さに比べて十分に小さく、核反応は真空中で起こるものとする。原子核および中性子は質点として扱い、量子的な波動性は無視できる。また、重力の影響は無視できるものとする。
Ⅰ.電子1個が1Vの電位差で加速されたときに得る運動エネルギーは1eVである。核反応で放出される核エネルギーを表すには、MeV(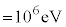 )という単位を用いるとわかりやすい。
)という単位を用いるとわかりやすい。
問6 1MeVは何Jか、有効数字2桁で求めよ。
問7 核反応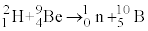 で放出される核エネルギーは何MeVか。以下の(ア)~(コ)の中から最も近いものを選んで記号で答えよ。
で放出される核エネルギーは何MeVか。以下の(ア)~(コ)の中から最も近いものを選んで記号で答えよ。 (ア) 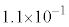 (イ)
(イ) 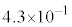 (ウ)
(ウ) 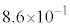 (エ)
(エ) 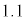
(オ) 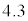 (カ)
(カ) 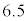 (キ)
(キ) 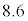 (ク)
(ク) 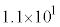
(ケ)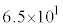 (コ)
(コ) 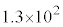
Ⅱ.原子核Xと原子核Yがx軸上で正面衝突し、核反応を起こして、中性子と原子核Zに変化した。その後、中性子と原子核Zはx軸上を運動した。最初、原子核Yはx軸上の原点に静止しており、原子核Xは静電気力を無視できるほど十分に原子核Yから離れた状態で、運動エネルギー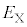 をもっていた。この核反応で放出される核エネルギーをQとする。
をもっていた。この核反応で放出される核エネルギーをQとする。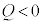 の場合は、
の場合は、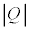 のエネルギーを外部から与えなければこの核反応は起こらない。
のエネルギーを外部から与えなければこの核反応は起こらない。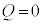 の場合には、この核反応による全核エネルギーの変化はない。
の場合には、この核反応による全核エネルギーの変化はない。
問8 以下の文章の に入るべき式や記号を、それぞれの{ }の中に与えられた文字や記号のうち必要なものを用いて表せ。
に入るべき式や記号を、それぞれの{ }の中に与えられた文字や記号のうち必要なものを用いて表せ。 原子核Xの質量を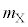 ,中性子の質量を
,中性子の質量を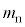 ,速度を
,速度を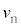 ,原子核Zの質量を
,原子核Zの質量を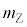 とすると、原子核Zの速度は、
とすると、原子核Zの速度は、  (1)
(1)と表せる。また、衝突後の全運動エネルギーが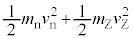 であることを用いると、核エネルギーも含めたエネルギー保存則より、衝突の前と後の全エネルギーが満たす関係は
であることを用いると、核エネルギーも含めたエネルギー保存則より、衝突の前と後の全エネルギーが満たす関係は 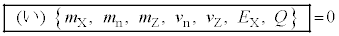 (2)
(2)となる。式(1)と式(2)より、この核反応が起こるために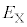 が満たすべき条件は
が満たすべき条件は  (3)
(3)となる。
一方で、原子核Xと原子核Yは共に正の電荷を持つので、核反応が起こるためには静電気力に逆らって両者が十分に接近する必要もある。このために必要な運動エネルギー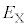 の最小値を
の最小値を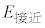 とする。
とする。
条件式(3)と条件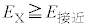 の両方が満たされたとき、またそのときに限り必ず核反応は起こるものとして以下の問に答えよ。
の両方が満たされたとき、またそのときに限り必ず核反応は起こるものとして以下の問に答えよ。
問9 核反応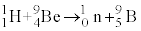 が起こり、中性子が発生した場合について考える。この核反応における
が起こり、中性子が発生した場合について考える。この核反応における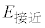 を1.00MeVとする。核反応が起こる前に、静電気力が無視できる十分に
を1.00MeVとする。核反応が起こる前に、静電気力が無視できる十分に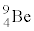 から離れた場所で、
から離れた場所で、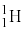 が持っていた運動エネルギーを
が持っていた運動エネルギーを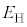 [MeV]とする。この核反応を起こすことができる運動エネルギー
[MeV]とする。この核反応を起こすことができる運動エネルギー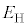 としてあてはまるものを、以下の(サ)~(タ)の中からすべて選んで記号で答えよ。必要ならば、
としてあてはまるものを、以下の(サ)~(タ)の中からすべて選んで記号で答えよ。必要ならば、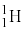 ,
,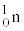 ,
,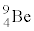 ,
,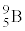 の質量がそれぞれ1.01u,1.01u,9.01u,9.01uであることを用いてもよい。
の質量がそれぞれ1.01u,1.01u,9.01u,9.01uであることを用いてもよい。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。