大学入学共通テスト数学IA 2026年問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1][1] 全体集合Uを2以上20以下の自然数全体の集合とする。すなわち
である。
2以上9以下の自然数a,bに対して、Uの部分集合A,Bを
とする。
例えば
である。
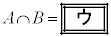 ,
,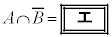
である。
 ~
~ の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)
(2) a,bが2以上9以下の自然数であることに注意して、a,bについて考えよう。
(i) 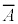 の要素に、2の倍数も3の倍数もないとき
の要素に、2の倍数も3の倍数もないとき である。
(ii) 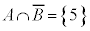 であるとき
であるとき 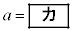 ,
,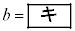
である。
[2] 以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(1) 四角形ABCDの面積Sについて考えよう。以下では、四角形ABCDの内角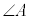 ,
,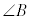 ,
,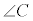 ,
,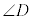 の大きさを、それぞれA,B,C,Dで表す。ただし、四つの内角はいずれも
の大きさを、それぞれA,B,C,Dで表す。ただし、四つの内角はいずれも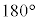 より小さいものとする。
より小さいものとする。 対角線BDを共通の1辺とする△ABDと△BCDの面積を、それぞれ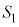 ,
,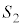 とすると、
とすると、 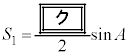 ,
,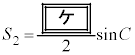
となる。
四角形ABCDの四つの内角が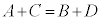 を満たすとき、
を満たすとき、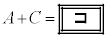 となる。このとき、
となる。このとき、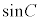 を
を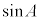 を用いて表せることに注意すると
を用いて表せることに注意すると 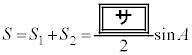 ・・・①
・・・①となる。
 ~
~ の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。)  の解答群
の解答群 の解答群
の解答群
(2) 点Oを中心とする半径6の円Oが、線分PQ上のP,Qと異なる点Mにおいて線分PQに接している。P,Qそれぞれを通る円Oの接線で、直線PQと異なるものを引き、この円との接点をそれぞれK,Lとする。以下では直線PK,QLが交わる場合を考え、その交点をRとする。このとき、△PQRの辺の長さについて考えよう。
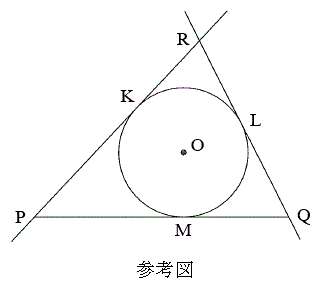 (i)
(i) 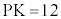 ,
,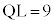 であるときを考え、
であるときを考え、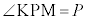 ,
,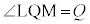 とする。このとき、2直線PK,QLの交点Rは直線PQに関して点Oと同じ側にある。
とする。このとき、2直線PK,QLの交点Rは直線PQに関して点Oと同じ側にある。四角形PMOKが△PMOと△PKOに分けられることに注意すると、四角形PMOKの面積は であることがわかる。このことから①を用いると、
であることがわかる。このことから①を用いると、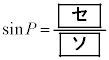 となることがわかる。
となることがわかる。
四角形QLOMについても同様に考えると、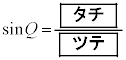 となることもわかる。よって、PR:QR =
となることもわかる。よって、PR:QR = 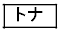 :
: となり、これにより
となり、これにより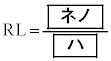 と求められるので、△PQRの辺の長さを求めることができる。
と求められるので、△PQRの辺の長さを求めることができる。
[解答へ]
[2][1] 2次関数の最大値、最小値について考えよう。
(1) 2次関数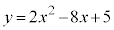 は
は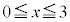 において、
において、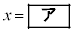 で最大値
で最大値 をとり、
をとり、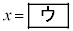 で最小値
で最小値 をとる。
をとる。
(2) 太郎さんと花子さんは、(1)を振り返って2次関数の最大値、最小値について話している。
太郎:(1)では、2次関数とxの取り得る値の範囲が与えられて、最大値と最小値を求めることができたね。
花子:じゃあ、xの値の範囲とそのときの最大値と最小値に関数条件が与えられている場合に、条件を満たす2次関数を求めることはできるのかな。具体的な例で考えてみよう。
(i) 2次関数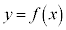 は次の条件1を満たすとする。
は次の条件1を満たすとする。
-条件1-----------------
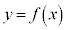 は
は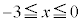 において
において・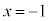 で最大値3をとる。
で最大値3をとる。 ・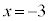 で最小値
で最小値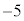 をとる。
をとる。 ---------------------
このとき、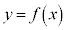 の頂点の座標は
の頂点の座標は であり、
であり、 である。
 の解答群
の解答群
(ii) 2次関数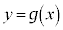 は次の条件2を満たすとする。
は次の条件2を満たすとする。
-条件2-----------------
aを正の定数とし、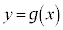 の
の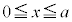 における最大値をM,最小値をmとすると
における最大値をM,最小値をmとすると ・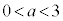 ならば、
ならば、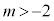 である。
である。 ・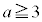 ならば、
ならば、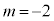 である。
である。 ・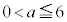 ならば、
ならば、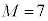 である。
である。 ・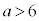 ならば、
ならば、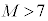 である。
である。 ---------------------
このとき、2次関数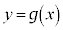 のグラフは
のグラフは の放物線であり
の放物線であり である。
 の解答群
の解答群  下に凸
下に凸  上に凸
上に凸 の解答群
の解答群
(3) 2次関数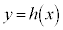 は次の条件3を満たすとする。
は次の条件3を満たすとする。
-条件3------------------
bを定数とし、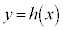 の
の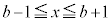 における最大値をMとすると
における最大値をMとすると ・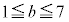 ならば、
ならば、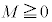 である。
である。 ----------------------
太郎さんと花子さんは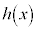 について話している。
について話している。
太郎:(2)の条件1や条件2からは関数が一つに決まったけど、条件3だけでは、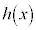 が一つに決まりそうにないね。
が一つに決まりそうにないね。 花子:でも、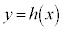 のグラフとx軸の共有点の座標はわかりそうだね。
のグラフとx軸の共有点の座標はわかりそうだね。
2次関数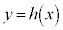 のグラフとx軸の共有点のx座標は
のグラフとx軸の共有点のx座標は および
および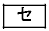 である。ただし、
である。ただし、 ,
, の解答の順序は問わない。
の解答の順序は問わない。
[2] 以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。
-----------------------
「(第1四分位数)-1.5×(四分位範囲)」以下の値
「(第3四分位数)+1.5×(四分位範囲)」以上の値
-----------------------
水泳部に所属する太郎さんは、1500m自由形におけるペース配分を考えるために、2021年に開催された東京オリンピックの男子1500m自由形に関するデータを分析することにした。なお、自由形とは、どのような泳ぎ方で泳いでもよい競技のことである。
分析で用いるデータは、28人の選手における、予選で計測された記録(以下、タイム)とする。ここでは、タイムは秒単位で表すものとする。例えば、15分23秒46であれば、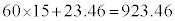 (秒)である。そして、公式順位(以下、順位)は、タイムの値が小さい方が上位となる。また、28人の選手それぞれのタイムについて、スタートから750mまでのタイムを
(秒)である。そして、公式順位(以下、順位)は、タイムの値が小さい方が上位となる。また、28人の選手それぞれのタイムについて、スタートから750mまでのタイムを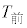 とし、750mからゴールまでのタイムを
とし、750mからゴールまでのタイムを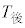 とする。さらに、
とする。さらに、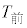 と
と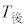 の平均値を
の平均値を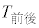 とする。
とする。
 (1) 太郎さんは、
(1) 太郎さんは、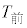 ,
,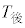 ,
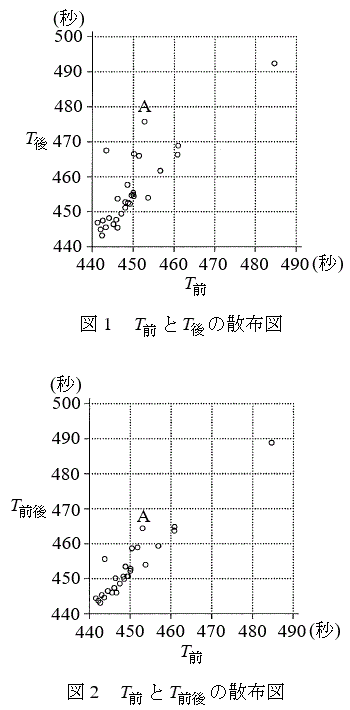
,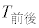 の関係を調べることにした。図1は
の関係を調べることにした。図1は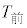 と
と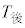 の散布図、図2は、
の散布図、図2は、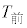 と
と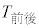 の散布図である。なお、これらの散布図には、完全に重なっている点はない。また、図1と図2において、Aを付している点は、同じ選手であることを表している。
の散布図である。なお、これらの散布図には、完全に重なっている点はない。また、図1と図2において、Aを付している点は、同じ選手であることを表している。
次の(a),(b)は、図1と図2に関する記述である。
(a) 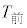 が470秒未満である選手について、
が470秒未満である選手について、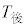 が460秒以上である選手の人数と、
が460秒以上である選手の人数と、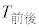 が460秒以上である選手の人数は等しい。
が460秒以上である選手の人数は等しい。 (b) Aを付している点が表す選手について、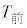 の値は
の値は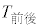 の値より小さく、かつ
の値より小さく、かつ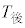 の値は
の値は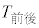 の値より大きい。
の値より大きい。 (a),(b)の正誤の組み合わせとして正しいものは である。
である。
 の解答群
の解答群
(2) 太郎さんは、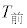 と
と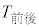 の相関係数を計算するために、表1のように、平均値、標準偏差および共分散を求めた。
の相関係数を計算するために、表1のように、平均値、標準偏差および共分散を求めた。 表1 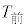 と
と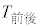 の平均値、標準偏差、共分散
の平均値、標準偏差、共分散
| | 平均値 | 標準偏差 | 共分散 |
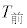 | 450 | 8.3 | 72.9 |
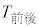 | 453 | 9.3 |
表1を用いると、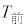 と
と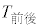 の相関係数は
の相関係数は である。
である。
 については、最も適当なものを、次の
については、最も適当なものを、次の ~
~ のうちから一つ選べ
のうちから一つ選べ  0.01
0.01  0.24
0.24  0.47
0.47  0.59
0.59  0.72
0.72 0.83
0.83  0.94
0.94 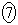 1.06
1.06 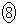 1.38
1.38 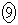 4.14
4.14
(3) 太郎さんは、順位とペース配分の関係を調べるために、前半と後半という二分割だけではなく、より細かく分割されたタイムを用いて分析することにした。1500m自由形のタイムは、スタートから50mまでのタイム、50mから100mまでのタイムのように、ゴールまで50mごとの30個に分けて計測されている。そこで、これら30個のタイムを用いて分析する。
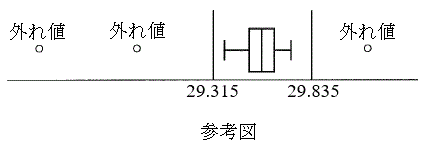 (i) 1位の選手の30個のタイムについて考えると、外れ値かどうかを判断する二つの値である29.315と29.835が算出され、29.315以下の2個のタイムと29.835以上の1個のタイムが外れ値と判断された。このとき、1位の選手の30個のタイムの四分位範囲は0.
(i) 1位の選手の30個のタイムについて考えると、外れ値かどうかを判断する二つの値である29.315と29.835が算出され、29.315以下の2個のタイムと29.835以上の1個のタイムが外れ値と判断された。このとき、1位の選手の30個のタイムの四分位範囲は0. 秒である。
秒である。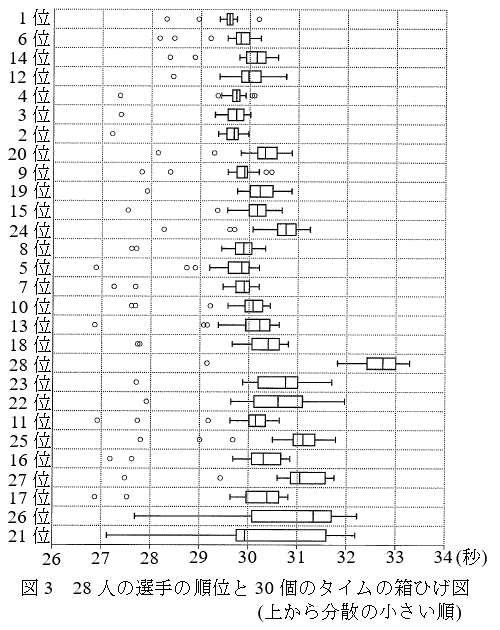 (ii) 太郎さんは28人の選手それぞれについて、30個のタイムを用いて、選手ごとの箱ひげ図を作成し、分散を計算した。図3は上から分散が小さくなるように、28人の選手それぞれの箱ひげ図を並べたものであり、30個のタイムにおける外れ値は、白丸で示されている。なお、分散が等しい選手はいなかった。
(ii) 太郎さんは28人の選手それぞれについて、30個のタイムを用いて、選手ごとの箱ひげ図を作成し、分散を計算した。図3は上から分散が小さくなるように、28人の選手それぞれの箱ひげ図を並べたものであり、30個のタイムにおける外れ値は、白丸で示されている。なお、分散が等しい選手はいなかった。
次の(a),(b)は、図3に関する記述である。
(a) 28人の選手について、29秒より速いタイムはすべて外れ値である。
(b) 28人の選手から2人を選んだとき、分散の大きい選手の四分位範囲は、分散の小さい選手の四分位範囲より小さいことがある。
(a),(b)の正誤の組み合わせとして正しいものは である。
である。
 の解答群
の解答群
(iii) 順位が1位から8位までの選手のグループを決勝進出グループ、9位から28位までの選手のグループを予選敗退グループと呼ぶことにする。決勝進出グループであり、かつ30個のタイムの分散が小さい方から14番目までの選手の人数をn(人)とすると、表2のようになる。
表2 順位と分散の表
| | 分散(小さい順) | 計 |
| 1番~14番 | 15番~28番 |
| 順位 | 決勝進出グループ | n | 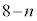 | 8 |
| 予選敗退グループ | 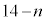 | 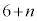 | 20 |
| 計 | 14 | 14 | 28 |
このとき、図3から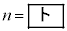 であることがわかる。このことから、決勝進出グループにおいて分散が小さい方から14番目の選手が占める割合をP,予選敗退グループにおいて分散が小さい方から14番目までの選手が占める割合をQとすると、
であることがわかる。このことから、決勝進出グループにおいて分散が小さい方から14番目の選手が占める割合をP,予選敗退グループにおいて分散が小さい方から14番目までの選手が占める割合をQとすると、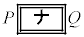 であることがわかる。
であることがわかる。
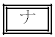 の解答群
の解答群
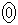 <
<  =
=  >
> [解答へ]
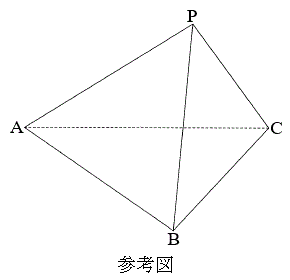 [3]空間内に、
[3]空間内に、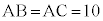 ,
,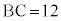 である二等辺三角形ABCがある。△ABCの内心をIとし、△IBCの重心をGとする。Gを通り、△ABCを含む平面と垂直な直線上に、Gと異なる点Pがある。このとき、△ABCを底面とする三角錐PABCについて考えよう。
である二等辺三角形ABCがある。△ABCの内心をIとし、△IBCの重心をGとする。Gを通り、△ABCを含む平面と垂直な直線上に、Gと異なる点Pがある。このとき、△ABCを底面とする三角錐PABCについて考えよう。
直線AIと辺BCの交点をDとし、また、辺PA上の点Eは、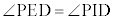 を満たしているとする。なお、以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
を満たしているとする。なお、以下の問題において比を解答する場合は、最も簡単な整数の比で答えよ。
(1) 直線BIが ことに注意すると、△ABDにおいて線分AIとIDの長さの比を求めることができる。よって、線分ADの長さに着目すると
ことに注意すると、△ABDにおいて線分AIとIDの長さの比を求めることができる。よって、線分ADの長さに着目すると 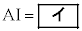 ,
,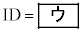
であることがわかる。また、4点E,I,D,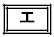 は同一円周上にある。よって
は同一円周上にある。よって であることがわかる。
 の解答群
の解答群  直線ACと垂直に交わる
直線ACと垂直に交わる
 直線ACとねじれの位置にある
直線ACとねじれの位置にある
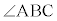 を2等分する
を2等分する
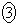 辺ACの中点を通る
辺ACの中点を通る の解答群
の解答群
(2) 線分PIとDEの交点をFとする。このとき、線分IFとFPの長さの比と、三角錐PABCび体積との関係について考えよう。
(i) 次の仮定1のもとで三角錐PABCの体積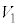 について考える。
について考える。
-仮定1-----------------
線分IFとFPの長さの比がIF:FP = 3:2である。
---------------------
このとき
PE:EA =  :
:
であるから、(1)での考察に注意すると、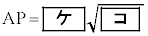 となる。
となる。
したがって、直線PGが△ABCを含む平面に垂直であることに注意すると、 であることがわかる。
であることがわかる。
(ii) (i)の仮定1の代わりに次の仮定2をおき、三角錐PABCの体積の変化について考える。
-仮定2-----------------
線分IFとFPの長さの比がIF:FP = 1:3である。
---------------------
仮定2のもとでの三角錐PABCの体積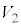 を、(i)で求めた
を、(i)で求めた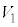 と比較すると、
と比較すると、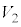 と
と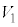 の比は
の比は であるから、 。
。
 の解答群
の解答群
[解答へ]
[4] 1人対1人で対戦する競技の大会があり、A,B,Cの3人、またはA,B,C,Dの4人で開催される。大会はリーグ戦形式で行われる。すなわち、それぞれの人が他の全ての人と1回ずつ対戦する。引き分けはないものとし、Aが対戦相手に勝つ確率は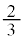 であり、A以外の2人が対戦するとき勝つ確率はどちらも
であり、A以外の2人が対戦するとき勝つ確率はどちらも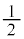 であるものとする。なお、各対戦の結果は互いに影響を与えないものとする。
であるものとする。なお、各対戦の結果は互いに影響を与えないものとする。
すべての対戦が終わった後、次の優勝者の決め方により優勝者を1人決める。
-優勝者の決め方--------------------
勝ち数が一番多い人が1人であれば、その人を優勝者とする。そうでなければ、抽選により、勝ち数が一番多い人の中から1人を選び、その人を優勝者とする。ただし、勝ち数が一番多い人の人数がn人であるとき、それぞれの人が選ばれる確率は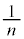 であるものとする。
であるものとする。 ---------------------------
Aが優勝する確率を、A,B,Cの3人でリーグ戦を行うときと、A,B,C,Dの4人でリーグ戦を行うときとで比較しよう。
以下では、すべての対戦の勝敗を対戦結果と呼ぶ。なお、対戦結果は抽選の結果を含まない。
対戦結果を示すために表を用いる。例えば、表1は4人でリーグ戦を行ったときの対戦結果の一つを示す。Aから始まる行の×〇〇は、AがBに負けCとDに勝ち、2勝1敗となったことを示す。また、勝ち数が一番多いAとBの2人が抽選の対象であり、そのことを✓で示す。
表 1
| \ | A | B | C | D | 勝ち数 | 負け数 | 抽選 |
| A | \ | × | 〇 | 〇 | 2 | 1 | ✓ |
| B | 〇 | \ | 〇 | × | 2 | 1 | ✓ |
| C | × | × | \ | 〇 | 1 | 2 | - |
| D | × | 〇 | × | \ | 1 | 2 | - |
(1) A,B,Cの3人でリーグ戦を行うときにAが優勝する確率を考える。
(i) Aが2勝0敗ならば、Aが優勝する。Aが2勝0敗で優勝する確率は である。
である。
(ii) Aが1勝1敗で優勝するためには、BもCも1勝1敗であることが必要である。例えば、Aが勝つ相手がBであるとき、AがCに負けBがCに勝つことが必要である。表2は、この対戦結果を示し、この対戦結果になる確率は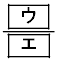 である。この対戦結果になり、かつAが抽選により優勝者に選ばれる確率は
である。この対戦結果になり、かつAが抽選により優勝者に選ばれる確率は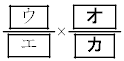 である。
である。
表 2
| \ | A | B | C | 勝ち数 | 負け数 | 抽選 |
| A | \ | 〇 | × | 1 | 1 | ✓ |
| B | × | \ | 〇 | 1 | 1 | ✓ |
| C | 〇 | × | \ | 1 | 1 | ✓ |
Aが勝つ相手はB,Cの2通りあることに注意すると、Aが1勝1敗で優勝する確率は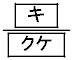 であることがわかる。(i)と(ii)から、Aが優勝する確率は
であることがわかる。(i)と(ii)から、Aが優勝する確率は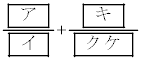 である。
である。
(2) A,B,C,Dの4人でリーグ戦を行うときにAが優勝する確率を考える。
Aが3勝0敗ならば、Aが優勝する。また、Aが1勝2敗ならば、2勝以上する人がいるためAは優勝しない。
Aが2勝1敗で優勝する確率を、全敗する人がいる場合の確率と全敗する人がいない場合の確率の和として求める。
(i) 全敗する人がいる場合で、かつAが2勝1敗で優勝する確率を求める。
全敗する人はB,C,Dの3通りある。例えば、Dが全敗するとき、対戦結果の一部を示すと表3のようになる。
表 3| \ | A | B | C | D | 勝ち数 | 負け数 | 抽選 |
| A | \ | | | 〇 | | | |
| B | | \ | | 〇 | | | |
| C | | | \ | 〇 | | | |
| D | × | × | × | \ | 0 | 3 | - |
Dが全敗する確率は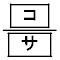 である。Dが全敗する場合、Aが2勝1敗で優勝するためには、AがD以外の2人との対戦で1勝1敗となることが必要である。
である。Dが全敗する場合、Aが2勝1敗で優勝するためには、AがD以外の2人との対戦で1勝1敗となることが必要である。
以上のことから、(1)の(ii)の結果を用い、全敗する人がB,C,Dの3通りあることに注意すると、全敗する人がいる場合で、かつAが2勝1敗で優勝する確率は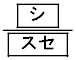 であることがわかる。
であることがわかる。
(ii) 全敗する人がいない場合で、かつAが2勝1敗で優勝する確率を求める。
Aが2勝1敗のとき、Aが負ける相手はB,C,Dの3通りある。例えば、Aが負ける相手がBであるとき、対戦結果の一部を示すと表4のようになる。
表 4| \ | A | B | C | D | 勝ち数 | 負け数 | 抽選 |
| A | \ | × | 〇 | 〇 | 2 | 1 | |
| B | 〇 | \ | | | | | |
| C | × | | \ | | | | |
| D | × | | | \ | | | |
このとき、
Aが優勝するためには、Bは2勝1敗か1勝2敗であることが必要である。例えば、表1は、AとBが2勝1敗である対戦結果の一つを示し、AとBの2人が抽選の対象となったことを示す。
表 1 (再掲)| \ | A | B | C | D | 勝ち数 | 負け数 | 抽選 |
| A | \ | × | 〇 | 〇 | 2 | 1 | ✓ |
| B | 〇 | \ | 〇 | × | 2 | 1 | ✓ |
| C | × | × | \ | 〇 | 1 | 2 | - |
| D | × | 〇 | × | \ | 1 | 2 | - |
全敗する人がいない場合で、かつAがBに負けCとDに勝ち優勝するときの対戦結果は 通りある。Aが負ける相手がB,C,Dの3通りあることに注意すると、全敗する人がいない場合で、かつAが2勝1敗で優勝する確率は
通りある。Aが負ける相手がB,C,Dの3通りあることに注意すると、全敗する人がいない場合で、かつAが2勝1敗で優勝する確率は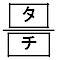 であることがわかる。
であることがわかる。
(i)と(ii)から、Aが2勝1敗で優勝する確率は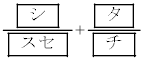 である。
である。
以上のことから、Aが3勝0敗で優勝する確率を考慮すると、Aが優勝する確率は であることがわかる。この確率は(1)で求めた3人でリーグ戦を行うときにAが優勝する確率より
であることがわかる。この確率は(1)で求めた3人でリーグ戦を行うときにAが優勝する確率より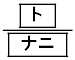 だけ
だけ 。
。
 の解答群
の解答群
 小さい
小さい  大きい
大きい
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2026(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。  ,
,
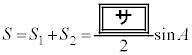 ・・・①
・・・①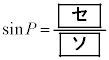 となることがわかる。
となることがわかる。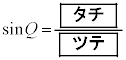 となることもわかる。よって、PR:QR =
となることもわかる。よって、PR:QR =  と求められるので、△PQRの辺の長さを求めることができる。
と求められるので、△PQRの辺の長さを求めることができる。 である。
である。 である。この対戦結果になり、かつAが抽選により優勝者に選ばれる確率は
である。この対戦結果になり、かつAが抽選により優勝者に選ばれる確率は である。
である。 であることがわかる。
であることがわかる。 である。
である。 である。Dが全敗する場合、Aが2勝1敗で優勝するためには、AがD以外の2人との対戦で1勝1敗となることが必要である。
である。Dが全敗する場合、Aが2勝1敗で優勝するためには、AがD以外の2人との対戦で1勝1敗となることが必要である。 であることがわかる。
であることがわかる。 であることがわかる。
であることがわかる。 である。
である。 であることがわかる。この確率は(1)で求めた3人でリーグ戦を行うときにAが優勝する確率より
であることがわかる。この確率は(1)で求めた3人でリーグ戦を行うときにAが優勝する確率より だけ
だけ